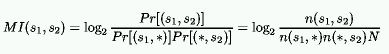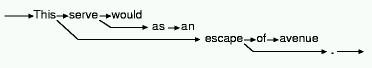[an error occurred while processing this directive]
[an error occurred while processing this directive]
Ñæàòèå ñ ïîìîùüþ ãðàììàòè÷åñêèõ ìîäåëåé
(compression using grammatical models)
Submission for DCC 1999
D R
A F T |
Lexical Attraction for Text
Compression |
Joscha Bach
Department of Computer Science,
Humboldt University
of Berlin,
Berlin, Germany
email: bach@informatik.hu-berlin.de |
Ian H. Witten
Department of Computer Science,
University of
Waikato,
Hamilton, New Zealand
email: ihw@cs.waikato.ac.nz
|
| Abstract
New methods of acquiring structural information in text documents may
support better compres sion by identifying an appropriate prediction
context for each symbol. The method of "lexical attraction" infers
syntactic dependency structures from statistical analysis of large
corpora. We describe the generation of a lexical attraction model, discuss
its application to text compression, and explore its potential to
outperform fixed-context models such as word-level PPM. Perhaps the most
exciting aspect of this work is the prospect of using compression as a
metric for structure discovery in text. |
1 Introduction
The most successful methods of text compression work by
conditioning each symbol's probability on its predecessors. Sequences of symbols
establish a context that determines a probability distribution for the next
symbol, and the actual next symbol is encoded with respect to this distribution.
For example, PPM uses the previous k symbols as context, for some small fixed
order k (Cleary and Witten, 1984). As is well known, the size of the model grows
exponentially with order. While fifth-order models are widely used for
character-based PPM, even second-order models are usually impractical for
word-level PPM because their alphabet includes many more symbols.
For textual documents written in natural language, it is obvious that there
are dependencies not only between adjacent symbols, but between more distant
words in a sentence. For example, verbs may depend on nouns, pronouns on names,
closing brackets on opening ones, question marks on "wh"-words. It is the
purpose of language grammars to characterize these dependency structures.
Grammars have some important limitations, apart from the practical difficulty
of finding natural language parsers that work robustly. First, they only
describe syntactically correct structures, and a grammar-based coder might fail
to predict many frequently-occurring phrases--even though, in most writing,
grammatically correct sentences are generally more likely than incorrect ones.
Second, although grammars capture syntactic structure, they do not necessarily
reflect typical language usage. Third, it is very difficult to derive
grammatical dependency structures for documents written in an unknown language.
The method of "lexical attraction," developed by Deniz Yuret (1998),
establishes dependency structures in textual documents based on the
co-occurrence of terms in a certain order in the same sentence, regardless of
the distance that separates them. This scheme is able to recognize linguistic
structure in text by organizing it in the form of a low-entropy model. Once
identified, the structure supports a more informed notion of context than simply
using the previous few characters or words. This context can be used for
prediction in much the same way as PPM.
Section 2 describes the idea of lexical attraction, particularly the measure
of mutual information on which it is founded, and explains the algorithm used to
acquire the dependency structure. Section 3 discusses how to encode textual
documents using the context provided by the lexical attraction model. Section 4
gives experimental results, and Section 5 draws some conclusions and suggests
directions for further improvement.
2 Lexical Attraction
This work is based on "link grammars," a new
formalism for natural language syntax in which sentences are parsed by
connecting their words together with links, or arcs (Sleator and Temperley,
1991; Lafferty et al., 1992). Links may be labeled by grammatical
structure relations (subject-verb and so on); we use an unsupervised learning
approach and therefore do not use (or generate) these labels.
Figure
1: The lexical attraction model for an example sentence from the Jefferson
corpus
For example, Figure 1 shows the linkage produced by our system for
the sentence This would serve as an avenue of escape. The first word,
This, links to the main verb serve and object escape. The
main verb is linked backward to the auxiliary would, and forward to
as. Escape is linked backward to of (and ideally,
avenue should have been linked back to an). Escape is also
linked forward to the period that ends the sentence. Throughout this paper,
tokens are words (they may include digits and non-punctuation printing
characters as well as letters) or individual characters of punctuation (period,
comma, semi-colon, colon, question mark, explanation mark, brackets, and
quotation marks); all contiguous white space is mapped into a single space
character.
Lexical attraction was developed in a recent Ph.D. thesis by Deniz Yuret
(1998) as a particular, concrete, methodology for discovering these linguistic
relations. Yuret suggests an unsuper vised learning method for inferring
dependency structures from a large corpus of natural language text. While his
work is aimed at natural language understanding, link grammars may have other
applications--such as compression modeling or topic extraction.
The lexical attraction of an ordered pair of words is the likelihood
that they will appear (in that order) within a sentence. This can be estimated
by counting the co-occurrences of word pairs. The resulting dependency structure
defines an undirected graph with words as vertices and links between them as
edges. The graph is chosen to maximize the lexical attraction between linked
items. Graphs are constructed to be planar--links do not cross--and we
capitalize upon this when creating them. Moreover, they are acyclic, which is a
necessary condition for the structure to be acquired.
2.1 Mutual information
When a pair of words is encoded together rather
than independently of each other, the coding gain is called mutual
information and measures the lexical attraction between the words. The
following example is taken from Yuret (1998).
In a certain corpus, the probability of the word Ireland is 0.0039%
and it may therefore be encoded in 14.65 bits. The probability of the word
Northern is 0.016%, or 12.60 bits. However, in 35.8% of all cases, the
word Northern precedes Ireland. This preceding Northern,
based on knowledge of the occurrence of the word Ireland, can be coded in
as little as 1.48 bits, for a gain in mutual information of 12.60 - 1.48 = 11.12
bits. Conversely, the probability of the word Ireland based on a previous
occurrence of Northern is 8.5%, leading to an encoding in 3.53 bits and a
gain of 11.12 bits. Note that the mutual information is the same irrespective of
the direction of the prediction. (It does, of course, depend on the word order:
the probability of Northern appearing after the word Ireland is
entirely different.)
Given the co-occurrence counts, the mutual information gained by encoding
words s1 and s2 together can be estimated as
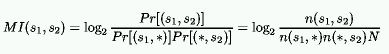bits, where n(s1,s2) is the number of times the pair has been
encountered, * is a wildcard matching every term, and N is the total number of
observations made. For practical purposes, the mutual information of a pair of
words that has been encountered two times or less is taken as zero.
2.2 Linking sentences
The most likely linkage for a sentence can be
found by generating all possible acyclic, planar graphs over it, and choosing
the one with the greatest accumulated lexical attraction--that is, the total
mutual information gain for all linked pairs of words. Unfortunately, the
computational complexity of this method is 0(n^5) for an n-word
sentence. Yuret (1998) proposes an approximate algorithm with a complexity of
O(n^2):
- for each word, consider linking it to each previous word in the sentence
in turn, starting with the preceding word;
- resolve conflicts created by cycles and crossing links by deleting the
weakest link in question.
(In fact, he suggests accepting only links with positive mutual
information, but we have not done this in our implementation because we seek a
fully-linked structure.)
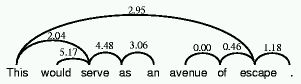
For example, when processing Figure 1 word by word, would is first
linked to this. Serve is then linked to this and
would; however, this creates a loop, so the weakest link (which happens
to be this-would) is deleted. As is linked to serve, and
then linking to would is attempted. As this would create a crossing link,
and because the link between this and serve is stronger, the
latter is retained instead. Linking as to this creates a cycle,
and because all other links in the cycle are at least as strong, the new link
cannot be established. And so the algorithm proceeds on down the sentence. The
numbers shown on each link give the mutual attraction of the word pairs for this
example sentence, calculated as described below. This algorithm may leave some
words disconnected when crossing links are broken, and as a final pass, every
unlinked word is connected to its direct predecessor.
2.3 Adaptive acquisition of mutual information
The mutual information
matrix for a corpus of text can be obtained by simply counting the co
occurrences of all pairs of words in each sentence, n(s1,s2), and
substituting into the formula above. Although this will produce good results in
the (very) long run, for corpora of moderate size it gives noisy estimates of
the probabilities. More reliable estimates can be obtained by making use of
previ ously identified links, leading to an adaptive scheme which takes
advantage of existing links to help create new ones (Yuret, 1998). As each
sentence of the corpus is processed, its dependency struc ture is derived from
the current set of probabilities. Then, counts are incremented only for certain
word pairs in the sentence, namely (a) adjacent pairs of words, (b) linked pairs
of words, and (c) the word pairs (A,Y) and (X,B) that occur in a
sequence XA ... BY where A and B have already been
connected. For example, in Figure 1 the counts associated with
this-would, this-serve, and this-as will be incremented for
reasons (a), (b) and (c) respectively.
An additional advantage of this counting scheme is that it generates much
smaller models than the brute force version, because fewer different pairs are
brought to the attention of the processor.
2.4 Results
Yuret trained his algorithm his algorithm on a reasonably
homogeneous corpus of 100 million words of Associated Press material. He
hand-parsed an independent test set of 200 sentences, and applied the lexical
attraction algorithm to them. Of the content-word pairs that were linked by
hand-parsing, 87.5% showed positive lexical attraction, which gives an upper
bound on what can be expected from this method. He also measured the quality of
the dependency structure in terms of recall and precision, again for links
between content-word pairs only. He found that 50% of content-word links in the
human-parsed test set were made by the algorithm (recall); and 60% of
content-word links established by the algorithm were present in the human-parsed
version (precision). Furthermore, his results suggest average mutual information
gains of up to 50% per link. It is expected that a smaller corpus, or a less
homogeneous one, will yield weaker links, reducing both precision and recall.
Yuret mentioned examples of the number of bits saved by encoding words based
on their links, and discussed an upper bound to the number of bits required to
transmit the linkage structure. How ever, he did not build a compression scheme
based on the lexical attraction idea, nor evaluate the linkage in terms of the
amount of compression that can be achieved.
3 Encoding based on lexical attraction
We have developed an encoding
scheme that takes a series of linked sentences like that of Figure 1 and
transmits them in the same manner as first-order word-level PPM. Of course, the
decoder needs additional information to restore the graph structure, and thus
establish the contexts for decompres sion. Unlike PPM, which performs only
forward prediction, a lexical attraction coder also predicts backwards. (The
situation becomes even more complicated with higher-order models, and we have
not considered them.) Indeed, word-level PPM is a special case where links are
made only between adjacent words.
3.1 Linking
Links across sentence boundaries connect the last term of
one sentence to the first term of the next. This makes sense (at least for
western languages) because the former is a punctuation mark that terminates the
sentence, while the latter is generally an upper-case word that is attracted to
the begin ning of sentences. Considering more than one sentence at a time might
lead to some improvement, because more links would be established between nouns
and related pronouns, opening and closing quotation marks, and so on.
In order to prime the lexical attraction linker, the whole document is
processed in advance to acquire the co-occurrence counts, and again in a second
pass to re-link the sentences. We have experimented with the use of multiple
passes, so that counts in one pass are based on sentences linked using the
statistics acquired in the previous one, but this does not yield any improvement
over the one-pass adaptive method described earlier.
As already noted, pairs that occur twice or less are not considered to have
significant lexical attraction, and so all terms that occur only once or twice
are excluded from the statistics. This significantly reduces the size of the
model, because in most corpora, about half the terms are hapax legomena
(words that appear only once).
The final output of the linking stage contains a triple for each word or item
of punctuation in the text: the index of the term, the index of the previous
term (the one that prediction is based on), and a flag indicating the relative
order of these terms (that is, whether it is a forward or a backward
prediction). Also, the graph structure of the document is recorded as described
below.
3.2 Adaptive encoding
To avoid the overhead that would be introduced by
the transmitting the complete model, the encoding stage utilizes an adaptive
PPM-style method. For each term acting as a predictor, two probability
distributions are maintained--one for forward and the other for backward
predictions. These are based on previously encoded pairs. For each pair
(p,q) of predicting and actual terms, the coder performs the following
steps.
- When p acts as a predictor for the first time, q is encoded
according to its zero-order probability (the number of times it appears in the
document divided by the total word count).
- If p does not include q in its predictions, an escape symbol
is sent, followed by the zero-order probability of q. The probability
of the escape symbol is given by Pr[esc]=r/(n+r) where n words
have been seen altogether in the context of the term p, and r of
them are distinct.
- Otherwise, the probability of q is estimated as Pr[q]=f(q)/n *
(1-Pr[esc]), where f(q) is the number of times that q has
appeared in the context of p.
- Finally, the models are updated. If the current encoding is based on a
forward prediction, the counts of f(q) in the forward context of
p and f(p) in the backward context of q are incremented.
Furthermore, the counts for the relevant r and n are incremented
in both models. In the case of a backward prediction, the backward and forward
roles are reversed.
This estimate for Pr[esc] implements the PPMC scheme
(Moffat, 1990). We have tried PPMD (Howard and Vitter, 1992), but find that it
yields no improvement.
3.3 Encoding the links
The baseline method of encoding the graph is to
enumerate all planar dependency structures on a sentence of n words, and
transmit the index of the actual graph. By counting the number of planar graphs,
an upper bound of 2.75 bits per term can be derived for the information
necessary to encode the graph (Yuret, 1998).
We reduce this figure by adopting the following strategy. Each sentence is
viewed as a tree, the root being the first word encoded. (More precisely, the
whole document is one large tree, because the last word of each sentence is
linked to the first word of the next.) To represent the structure of this tree,
it is sufficient to record the number of forward and backward links for each
word (ignoring the link to the previous word). Once the link counts have been
communicated, the words can be transmitted recursively, from left to right.
Figure
2a: Encoding the link structure: successor and predecessor counts
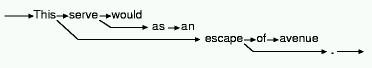
Figure
2b: Transmission order
Figure 2a shows the link counts, and Figure 2b gives the
transmission order for the sentence. The order is easily derived from the
counts. The first word, This, is sent first. It has two forward links,
the first of which, serve, is sent next. Before the second forward link
(escape) is sent, however, the word serve is processed. It has one
backward and one forward link. The former, would, is sent first. Its link
counts are zero, so we unwind to continue the processing of serve by
sending its forward link, as. This term has a backward count of zero and
a forward count of one, so an is sent next. Since this has zero link
counts, we unwind to continue the processing of This by sending the word
escape.
In order to transmit the link counts, each different pair of numbers for
forward and backward links is treated as a single symbol, and the resulting
sequence is compressed using PPMD. For the texts we have worked with,
transmitting the graph structure in this way imposes an overhead of around 2.3
bits/term.
3.4 Trading graph uniformity for mutual information
The number of bits
required by a lexical attraction compressor to encode text is the information
necessary to transmit the dependency graph, plus the actual information content
of the terms. Un fortunately, encoding the graph imposes significant overhead,
and overall performance may be even worse than zero-order encoding--particularly
on small corpora. The overhead can be artificially re duced by generating a link
structure with greater uniformity. Of course, the price is paid for this is a
reduction in effective mutual information.
The most frequent link combination consists of no backward links and one
forward link--that is, a forward link from one term to the next, recording the
standard reading order. The graph can be simplified to favor adjacent links by
deleting links between non-adjacent terms if their mutual information gain is
insignificant. We do this only in the second pass through the document, when the
sentences are linked in final form, not in the first pass which accumulates the
probability information.
In the extreme, when only links to adjacent terms are accepted, links reflect
the natural word order and the coder's output is the same as first-order PPM. In
this case, the overhead of transmitting the graph structure is negligible
because only one count pair occurs, (0, 1). Then first-order PPM becomes a
special case of (first-order) lexical attraction encoding.
4 Experimental results
Since most words in English have low frequency
counts, the acquisition of mutual information depends heavily on corpus size.
Best results for a lexical attraction compressor are obtained using a
homogeneous corpus of very large size. The largest one we could obtain is
Jefferson the Virginian (Malone, 1948), which we have available as a 6.3
Mbyte ASCII file. Most experiments were undertaken on this. It contains a total
of 1,238,973 words, which we segmented into 50,729 sentences using
straightforward methods. Each punctuation mark was considered to be a term, and
all terms are separated by a single space.
Encouraging results have been achieved with this corpus. However, further
work with larger corpora is necessary to explore the limits of compression that
are achievable using lexical attraction.
4.1 Acquiring mutual information
The acquisition of mutual information
depends on two factors: the size of the corpus and its compo sition in terms of
homogeneity, vocabulary, and sentence length. We investigate these separately.
4.1.1 Size of corpus
We begin by examining how the first-order entropy
depends on text size, when the entropy is calculated based on the appropriate
word in the lexical dependency graph, and when it is calculated based on the
preceding word. Figure 3 shows the text size in words along the horizontal axis,
for the first 2^11, 2^12, etc, words of Jefferson the Virginian. The
vertical axis expresses the gain in entropy as a percentage of the entropy of a
zero-order model of the same text. In the upper line the first-order entropy is
calculated based on the appropriate word of the dependency graph; note that this
corresponds to the mutual information of the text, except that it is calculated
adaptively rather than statically. The lower line uses the preceding word as
context, as in ordinary first-order PPM. The horizontal scale is logarithmic:
the size of the text doubles at each step.
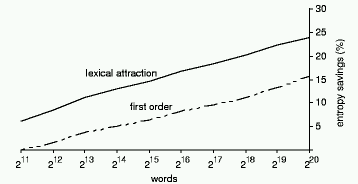
Figure
3: First-order entropy expressed as the percentage saved over a zero-order
model
As expected, the entropy savings are larger for the lexical
attraction model than for a plain first order one. With a text of 2^16 words,
for example, the ordinary first-order model gains 8% over the zero-order one,
while the lexical attraction model gains 17%. After 1.2 million words have been
encountered, lexical attraction shows an improvement of 24%, and if the corpus
were to grow further even better results would be obtained as more dependency
structure is acquired. Of course, the graph will eventually flatten out with a
sufficiently large homogeneous corpus--but it would have to be astronomically
large.
However, this is not the whole story: these figures omit the overhead of
transmitting the graph structure. We will see below that this significantly
reduces the overall compression achieved.
4.1.2 Composition of corpus
In order to further investigate the effect
of the size and composition of the corpus, we performed subsidiary experiments
on three other bodies of text. One is derived from the Gutenberg project, which
is making public-domain English literature available in machine-readable form.
This corpus contains a wide variety of very different documents, and we used a
subset containing 137 books, or 27 million words, of English prose. The second
body of text, Thomas Hardy's Far from the Madding Crowd, is small but far
more homogeneous than Gutenberg. Finally we used a corpus of children's language
consisting of extremely short and simple sentences.
Table 1 shows the size of these corpora, the number of different words they
contain, and the zero order entropy. The inhomogeneity of the Gutenberg corpus
can be seen from its disproportionately large vocabulary, although this does not
result in a significantly increased zero-order entropy. Far from the madding
crowd is both much smaller, and more homogeneous. The children's language
corpus exhibits a tiny vocabulary and a correspondingly low zero-order entropy.
| corpus |
size (words) |
vocabulary (words) |
zero-order (bits/word) |
lexical attraction (bits/word) |
savings over zero-order model |
| Gutenberg (extracts) |
26,636,000 |
264,000 |
9.97 |
8.15 |
18.2% |
| Far from the madding crowd |
168,000 |
14,000 |
9.22 |
7.51 |
18.5% |
| Jefferson the Virginian |
1,239,000 |
29,000 |
9.47 |
7.24 |
23.6% |
| Children's language |
184,000 |
4,700 |
7.87 |
5.84 |
25.8% |
Table 1: Results of experiments
on different corpora
The last two columns of Table 1 give the results of our experiments on these
corpora, in terms of the first-order entropy of the lexical attraction model,
and the percentage savings it yields over the zero-order entropy. Far from
the madding crowd gives the same percentage savings as Gutenberg, despite
being a tiny fraction of the size. Clearly quality--homogeneity--makes up for
quantity, and the savings are about the same as Figure 1 shows for a
similarly-sized extract from Jefferson the Virginian. The third row
illustrates how better linkage structures are discovered as the text grows,
while the result for children's language demonstrates that comparable savings
can be achieved from a far smaller corpus if the linguistic structure is simple
enough.
4.2 Encoding the graph
We now turn to the information content of the
dependency graph. For a naive enumerative encod ing, this depends heavily on the
average sentence length. However, our coding method (described above, using
third-order PPMD) greatly reduces this effect. Table 2 shows the results, which
range from 2.38 bits/term for the Gutenberg corpus to 1.61 bits/term for the
children's language corpus. The per-term entropy of the graph is reasonably
independent of the size of the document and its vocabulary--although it will be
lower if the document is too small to establish a complex depen dency structure.
Table 2 also shows the total entropy per term, taking into account both the
encoding of the dependency graph and the first-order entropy based on its
predictions.
| corpus |
average sentence length |
graph encoding (bits/term) |
lexical attraction (bits/term) |
| Gutenberg (extracts) |
15.3 |
2.38 |
10.53 |
| Far from the madding crowd |
13.8 |
2.31 |
9.82 |
| Jefferson the Virginian |
24.4 |
2.35 |
9.59 |
| Children's language |
6.2 |
1.61 |
7.45 |
Table 2: Information required to
encode the dependency graph
4.3 Results of lexical attraction encoding
Next we look at how overall
compression for the lexical attraction method depends on text size, and compare
it with zero- and first-order coders. Figure 4 plots the compression rate for
these three methods against text size for Jefferson the Virginian, along
with (at the bottom) the rate for lexical attraction without taking the graph
structure into account. Because of the overhead of transmitting the dependency
graph, lexical attraction gives worse compression than a zero-order model right
up to texts of a million or so words. At that point it overtakes zero-order
modeling. Unfortunately for lexical attraction, it is beaten hands down by
first-order compression up to a million words--although a generous eye can
discern a more favorable trend for larger text sizes.
Figure
4: Compression by lexical attraction , compared with zero- and first-order
coding
4.4 Simplifying the graph
Results for lexical attraction can be improved
by penalizing links between non-adjacent words as mentioned above. Varying the
penalty yields a smooth transition from lexical attraction to a first order
model, illustrated in Figure 5. If the encoder is prevented from linking
non-adjacent words, the gain from mutual information drops, but the number of
bits necessary to encode the graph structure decreases too. When only adjacent
pairs are linked, the graph can be encoded using no bits at all, but the mutual
information is the same as for first-order PPM. Another way of reducing the
entropy of the graph is to artificially limit the number of links per word.
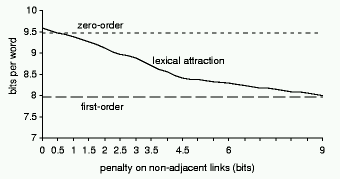
Figure
5: The effect on compression of penalizing non-adjacent links
5 Conclusions
The best predictors for individual words of text are not
necessarily their immediate predecessors. Measuring the lexical attraction
between terms is a way of identifying dependency structures that define a
low-entropy representation of the text. This paper has investigated this
phenomenon and shown how lexical attraction can be applied for the purposes of
text compression. Our experimental results are somewhat disappointing, for they
show that first-order lexical attraction is out-performed by first-order PPM
even on fairly large texts, rendering it useless for most practical purposes.
How ever, it can be extended to subsume PPM, and thereby perform at the same
level with an appropriate parameter setting.
The disappointing performance can be traced to the need to encode the
dependency graph and transmit it to the decoder. In the current implementation,
little attempt has been made to refine the encoding of the graph structure. But
there are many opportunities for improvement. It is likely, for example, that
many words have significant correlation with their position and link structure.
The graph could be broken at points where the lexical attraction between two
words is negative, and a zero-order encoding of the term in question used
instead. Links over sentence boundaries could be introduced, improving the gains
that can be achieved by linking between words.
Work with larger corpora will be necessary to explore the limits to the gains
achievable by mutual attraction, a completely open question at present.
Performance enhancements could be made simply by priming the compressor with
standard corpora, and introducing ways to counter inhomogeneity by priming
sub-contexts for structurally different passages of the text--for instance
poems, formulas or entirely alien documents. Finally, a higher-order compression
scheme could be developed to capture relations between groups of words.
We feel that lexical attraction is a promising new method for text
compression, and expect that ultimately, lexical attraction coders will
consistently out-perform standard prior-context models. Per haps the most
exciting aspect is the prospect of uncovering more and more structure in text as
it is compressed, and the use of compression to measure the success of structure
discovery.
Acknowledgments
We gratefully acknowledge stimulating discussions with
Tony Smith on lexical attraction. Thanks to Deniz Yuret for writing the thesis
that started the whole thing off, and helping us to understand some of the
details; to Bill Teahan for making available the Jefferson text; and to Stuart
Inglis for technical help.
References
[1] Cleary, J.G. and Witten, I.H. (1984) "Data compression
using adaptive coding and partial string matching." IEEE Trans Communications,
Vol. COM-32, No. 4, pp. 396-402.
[2] Howard, P.G. and Vitter, J.S. (1992) "Practical implementations of
arithmetic coding." In Image and Text Compression, edited by J.A. Storer. Kluwer
Academic Publishers, pp. 113-144.
[3] Lafferty, J.D., Sleator, D. and Temperley, D. (1992) "Grammatical
trigrams: A probabilistic model of link grammar." Proc AAAI Fall Symposium on
Probabilistic Approaches to Natural Language, Cambridge, MA, pp. 89-97.
[4] Malone, D. (1948) Jefferson the Virginian. Little Brown and Co., Boston.
[5] Moffat, A. (1990) "Implementing the PPM data compression scheme." IEEE
Transactions on Communications, Vol. 38, No. 11, pp. 1917-1921.
[6] Sleator, D. and Temperley, D. (1991) "Parsing English with a link
grammar." Technical Report CMU-CS-91-196, Department of Computer Science,
Carnegie Mellon University.
[7] Yuret, D. (1998) "Discovery of linguistic relations using lexical
attraction." PhD Thesis, Depart ment of Computer Science and Electrical
Engineering, MIT; May.
Joscha Bach
Last altered: 20
Nov 98
íàâåðõ
[an error occurred while processing this directive]