Код Хаффмана
Симаков Александр
Сыктывкарский Государственный Университет
Кафедра Прикладной Математики
Введение
В этой статье мы рассмотрим один из самых распространенных методов сжатия данных. Речь пойдет о коде Хаффмана (Huffman code) или минимально-избыточном префиксном коде (minimum-redundancy prefix code). Мы начнем с основных идей кода Хаффмана, исследуем ряд важных свойств и затем приведем полную реализацию кодера и декодера, построенных на идеях, изложенных в этой статье.
Идея, лежащая в основе кода Хаффмана, достаточно проста. Вместо того чтобы кодировать все символы одинаковым числом бит (как это сделано, например, в ASCII кодировке, где на каждый символ отводится ровно по 8 бит), будем кодировать символы, которые встречаются чаще, меньшим числом бит, чем те, которые встречаются реже. Более того, потребуем, чтобы код был оптимален или, другими словами, минимально-избыточен.
Первым такой алгоритм опубликовал Дэвид Хаффман (David Huffman) [1] в 1952 году. Алгоритм Хаффмана двухпроходный. На первом проходе строится частотный словарь и генерируются коды. На втором проходе происходит непосредственно кодирование.
Стоит отметить, что за 50 лет со дня опубликования, код Хаффмана ничуть не потерял своей актуальности и значимости. Так с уверенностью можно сказать, что мы сталкиваемся с ним, в той или иной форме (дело в том, что код Хаффмана редко используется отдельно, чаще работая в связке с другими алгоритмами), практически каждый раз, когда архивируем файлы, смотрим фотографии, фильмы, посылаем факс или слушаем музыку.
Код Хаффмана
Определение 1: Пусть A={a1,a2,...,an} - алфавит из n различных символов, W={w1,w2,...,wn} - соответствующий ему набор положительных целых весов. Тогда набор бинарных кодов C={c1,c2,...,cn}, такой что:
| (1) | ci не является префиксом для cj, при i!=j |
| (2) | 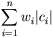 |
минимальна (|ci| длина кода ci) |
Замечания:
- Свойство (1) называется свойством префиксности. Оно позволяет однозначно декодировать коды переменной длины.
- Сумму в свойстве (2) можно трактовать как размер закодированных данных в битах. На практике это очень удобно, т.к. позволяет оценить степень сжатия не прибегая непосредственно к кодированию.
- В дальнейшем, чтобы избежать недоразумений, под кодом будем понимать битовую строку определенной длины, а под минимально-избыточным кодом или кодом Хаффмана - множество кодов (битовых строк), соответствующих определенным символам и обладающих определенными свойствами.
Известно, что любому бинарному префиксному коду соответствует определенное бинарное дерево.
Определение 2: Бинарное дерево, соответствующее коду Хаффмана, будем называть деревом Хаффмана.
Задача построения кода Хаффмана равносильна задаче построения соответствующего ему дерева. Приведем общую схему построения дерева Хаффмана:
- Составим список кодируемых символов (при этом будем рассматривать каждый символ как одноэлементное бинарное дерево, вес которого равен весу символа).
- Из списка выберем 2 узла с наименьшим весом.
- Сформируем новый узел и присоединим к нему, в качестве дочерних, два узла выбранных из списка. При этом вес сформированного узла положим равным сумме весов дочерних узлов.
- Добавим сформированный узел к списку.
- Если в списке больше одного узла, то повторить 2-5.
Приведем пример: построим дерево Хаффмана для сообщения S="A H F B H C E H E H C E A H D C E E H H H C H H H D E G H G G E H C H H".
Для начала введем несколько обозначений:
- Символы кодируемого алфавита будем выделять жирным шрифтом: A, B, C.
- Веса узлов будем обозначать нижними индексами: A5, B3, C7.
- Составные узлы будем заключать в скобки: ((A5+B3)8+C7)15.
Итак, в нашем случае A={A, B, C, D, E, F, G, H}, W={2, 1, 5, 2, 7, 1, 3, 15}.
- A2 B1 C5 D2 E7 F1 G3 H15
- A2 C5 D2 E7 G3 H15 (F1+B1)2
- C5 E7 G3 H15 (F1+B1)2 (A2+D2)4
- C5 E7 H15 (A2+D2)4 ((F1+B1)2+G3)5
- E7 H15 ((F1+B1)2+G3)5 (C5+(A2+D2)4)9
- H15 (C5+(A2+D2)4)9 (((F1+B1)2+G3) 5+E7)12
- H15 ((C5+(A2+D2)4) 9+(((F1+B1)2+G3) 5+E7)12)21
- (((C5+(A2+D2)4) 9+(((F1+B1)2+G3) 5+E7)12)21+H15)36
В списке, как и требовалось, остался всего один узел. Дерево Хаффмана построено. Теперь запишем его в более привычном для нас виде.
ROOT
/\
0 1
/ \
/\ H
/ \
/ \
/ \
0 1
/ \
/ \
/ \
/ \
/\ /\
0 1 0 1
/ \ / \
C /\ /\ E
0 1 0 1
/ \ / \
A D /\ G
0 1
/ \
F B
Листовые узлы дерева Хаффмана соответствуют символам кодируемого алфавита. Глубина листовых узлов равна длине кода соответствующих символов.
Путь от корня дерева к листовому узлу можно представить в виде битовой строки, в которой "0" соответствует выбору левого поддерева, а "1" - правого. Используя этот механизм, мы без труда можем присвоить коды всем символам кодируемого алфавита. Выпишем, к примеру, коды для всех символов в нашем примере:
| A=0010bin | C=000bin | E=011bin | G=0101bin |
| B=01001bin | D=0011bin | F=01000bin | H=1bin |
Теперь у нас есть все необходимое для того чтобы закодировать сообщение S. Достаточно просто заменить каждый символ соответствующим ему кодом:
S/="0010 1 01000 01001 1 000 011 1 011 1 000 011 0010 1 0011 000 011 011 1 1 1 000 1 1 1 0011 011 0101 1 0101 0101 011 1 000 1 1".
Оценим теперь степень сжатия. В исходном сообщении S было 36 символов, на каждый из которых отводилось по [log2|A|]=3 бита (здесь и далее будем понимать квадратные скобки [] как целую часть, округленную в положительную сторону, т.е. [3,018]=4). Таким образом, размер S равен 36*3=108 бит
Размер закодированного сообщения S/ можно получить воспользовавшись замечанием 2 к определению 1, или непосредственно, подсчитав количество бит в S/. И в том и другом случае мы получим 89 бит.
Итак, нам удалось сжать 108 в 89 бит.
Теперь декодируем сообщение S/. Начиная с корня дерева будем двигаться вниз, выбирая левое поддерево, если очередной бит в потоке равен "0", и правое - если "1". Дойдя до листового узла мы декодируем соответствующий ему символ.
Ясно, что следуя этому алгоритму мы в точности получим исходное сообщение S.
Канонический код Хаффмана
Как можно было заметить из предыдущего раздела, код Хаффмана не единственен. Мы можем подвергать его любым трансформациям без ущерба для эффективности при соблюдении всего двух условий: коды должны остаться префиксными и их длины не должны измениться.
Определение 3:
Код Хаффмана D={d1,d2,...,dn}
называется каноническим [2], если:
(1) Короткие коды (если их дополнить нулями справа) численно больше длинных,
(2) Коды одинаковой длины численно возрастают вместе с алфавитом.
Далее, для краткости, будем называть канонический код Хаффмана просто каноническим кодом.
Определение 4: Бинарное дерево, соответствующее каноническому коду Хаффмана, будем называть каноническим деревом Хаффмана.
В качестве примера приведем каноническое дерево Хаффмана для сообщения S, и сравним его с обычным деревом Хаффмана.
ROOT
/\
0 1
/ \
/\ H
/ \
/ \
0 1
/ \
/ \
/ \
/\ /\
/ \ / \
0 1 0 1
/ \ / \
/ \ / \
/\ /\ C E
0 1 0 1
/ \ / \
/\ A D G
0 1
/ \
B F
Выпишем теперь канонические коды для всех символов нашего алфавита в двоичной и десятичной форме. При этом сгруппируем символы по длине кода.
| B=00000bin=0dec | A=0001bin=1dec | C=010bin=2dec | H=1bin=1dec |
| F=00001bin=1dec | D=0010bin=2dec | E=011bin=3dec | |
| G=0011bin=3dec |
Убедимся в том, что свойства (1) и (2) из определения 3 выполняются:
Рассмотрим, к примеру, два символа: E и G. Дополним код символа E=011bin=3dec (максимальная_длина_кода-длина_кода)=5-3=2 нулями справа: E/=011 00bin=12dec, аналогично получим G/=0011 0bin=6dec. Видно что E/>G/.
Рассмотрим теперь три символа: A, D, G. Все они имеют код одной длины. Лексикографически A<D<G. В таком же отношении находятся и их коды: 1<2<3.
Далее заметим, что порядковый номер любого листового узла, на занимаемом им уровне, численно равен коду соответствующего ему символа. Это свойство канонических кодов называют числовым (Numerical property).
Поясним вышесказанное на примере. Рассмотрим символ C. Он находится на 3м уровне (имеет длину кода 3). Его порядковый номер на этом уровне равен 2 (учитывая два нелистовых узла слева), т.е. численно равен коду символа C. Теперь запишем этот номер в двоичной форме и дополним его нулевым битом слева (т.к. 2 представляется двумя битами, а код символа C тремя): 2dec=10bin=>0 10bin. Мы получили в точности код символа C.
Таким образом, мы пришли к очень важному выводу: канонические коды вполне определяются своими длинами. Это свойство канонических кодов очень широко используется на практике. Мы к нему еще вернемся.
Теперь вновь закодируем сообщение S, но уже при помощи канонических кодов:
Z/="0001 1 00001 00000 1 010 011 1 011 1 010 011 0001 1 0010 010 011 011 1 1 1 010 1 1 1 0010 011 0011 1 0011 0011 011 1 010 1 1"
Т.к. мы не изменили длин кодов, размер закодированного сообщения не изменился: |S/|=|Z/|=89 бит.
Теперь декодируем сообщение Z/, используя свойства канонических кодов.
Построим три массива: base[], symb[], offs[]. Где base[i] - количество нелистовых узлов на уровне i; symb[] - перестановка символов алфавита, отсортированная по двум ключам: первичный - длина кода, вторичный - лексикографическое значение; offs[i] - индекс массива symb[], такой что symb[offs[i]] первый листовой узел (символ) на уровне i.
В нашем случае: base[0..5]={?, 1, 2, 2, 1, 0}, symb[0..7]={B, F, A, D, G, C, E, H}, offs[0..5]={?, 7, ?, 5, 2, 0}.
Приведем несколько пояснений. base[0]=? и offs[0]=? не используются, т.к. нет кодов длины 0, а offs[2]=? - т.к. на втором уровне нет листовых узлов.
Теперь приведем алгоритм декодирования (CANONICAL_DECODE) [5]:
- code = следующий бит из потока, length = 1
- Пока code < base[length]
code = code << 1
code = code + следующий бит из потока
length = length + 1 - symbol = symb[offs[length] + code - base[length]]
Другими словами, будем вдвигать слева в переменную code бит за битом из входного потока, до тех пор, пока code < base[length]. При этом на каждой итерации будем увеличивать переменную length на 1 (т.е. продвигаться вниз по дереву). Цикл в (2) остановится когда мы определим длину кода (уровень в дереве, на котором находится искомый символ). Остается лишь определить какой именно символ на этом уровне нам нужен.
Предположим, что цикл в (2), после нескольких итераций, остановился. В этом случае выражение (code - base[length]) суть порядковый номер искомого узла (символа) на уровне length. Первый узел (символ), находящийся на уровне length в дереве, расположен в массиве symb[] по индексу offs[length]. Но нас интересует не первый символ, а символ под номером (code - base[length]). Поэтому индекс искомого символа в массиве symb[] равен (offs[length] + (code - base[length])). Иначе говоря, искомый символ symbol=symb[offs[length] + code - base[length]].
Приведем конкретный пример. Пользуясь изложенным алгоритмом декодируем сообщение Z/.
Z/="0001 1 00001 00000 1 010 011 1 011 1 010 011 0001 1 0010 010 011 011 1 1 1 010 1 1 1 0010 011 0011 1 0011 0011 011 1 010 1 1"
- code = 0, length = 1
- code = 0 < base[length] = 1
code = 0 << 1 = 0
code = 0 + 0 = 0
length = 1 + 1 = 2
code = 0 < base[length] = 2
code = 0 << 1 = 0
code = 0 + 0 = 0
length = 2 + 1 = 3
code = 0 < base[length] = 2
code = 0 << 1 = 0
code = 0 + 1 = 1
length = 3 + 1 = 4
code = 1 = base[length] = 1
- symbol = symb[offs[length] = 2 + code = 1 - base[length] = 1] = symb[2] = A
- code = 1, length = 1
- code = 1 = base[length] = 1
- symbol = symb[offs[length] = 7 + code = 1 - base[length] = 1] = symb[7] = H
- code = 0, length = 1
- code = 0 < base[length] = 1
code = 0 << 1 = 0
code = 0 + 0 = 0
length = 1 + 1 = 2
code = 0 < base[length] = 2
code = 0 << 1 = 0
code = 0 + 0 = 0
length = 2 + 1 = 3
code = 0 < base[length] = 2
code = 0 << 1 = 0
code = 0 + 0 = 0
length = 3 + 1 = 4
code = 0 < base[length] = 1
code = 0 << 1 = 0
code = 0 + 1 = 1
length = 4 + 1 = 5
code = 1 > base[length] = 0
- symbol = symb[offs[length] = 0 + code = 1 - base[length] = 0] = symb[1] = F
Итак, мы декодировали 3 первых символа: A, H, F. Ясно, что следуя этому алгоритму мы получим в точности сообщение S.
Это, пожалуй, самый простой алгоритм для декодирования канонических кодов. К нему можно придумать массу усовершенствований. Подробнее о них можно прочитать в [5] и [9].
Вычисление длин кодов
Для того чтобы закодировать сообщение нам необходимо знать коды символов и их длины. Как уже было отмечено в предыдущем разделе, канонические коды вполне определяются своими длинами. Таким образом, наша главная задача заключается в вычислении длин кодов.
Оказывается, что эта задача, в подавляющем большинстве случаев, не требует построения дерева Хаффмана в явном виде. Более того, алгоритмы использующие внутреннее (не явное) представление дерева Хаффмана оказываются гораздо эффективнее в отношении скорости работы и затрат памяти.
На сегодняшний день существует множество эффективных алгоритмов вычисления длин кодов ([3], [4]). Мы ограничимся рассмотрением лишь одного из них. Этот алгоритм достаточно прост, но несмотря на это очень популярен. Он используется в таких программах как zip, gzip, pkzip, bzip2 и многих других.
Вернемся к алгоритму построения дерева Хаффмана. На каждой итерации мы производили линейный поиск двух узлов с наименьшим весом. Ясно, что для этой цели больше подходит очередь приоритетов, такая как пирамида (минимальная). Узел с наименьшим весом при этом будет иметь наивысший приоритет и находиться на вершине пирамиды. Приведем этот алгоритм.
- Включим все кодируемые символы в пирамиду.
- Последовательно извлечем из пирамиды 2 узла (это будут два узла с наименьшим весом).
- Сформируем новый узел и присоединим к нему, в качестве дочерних, два узла взятых из пирамиды. При этом вес сформированного узла положим равным сумме весов дочерних узлов.
- Включим сформированный узел в пирамиду.
- Если в пирамиде больше одного узла, то повторить 2-5.
Будем считать, что для каждого узла сохранен указатель на его родителя. У корня дерева этот указатель положим равным NULL. Выберем теперь листовой узел (символ) и следуя сохраненным указателям будем подниматься вверх по дереву до тех пор, пока очередной указатель не станет равен NULL. Последнее условие означает, что мы добрались до корня дерева. Ясно, что число переходов с уровня на уровень равно глубине листового узла (символа), а следовательно и длине его кода. Обойдя таким образом все узлы (символы), мы получим длины их кодов.
Максимальная длина кода
Как правило, при кодировании используется так называемая кодовая книга (CodeBook), простая структура данных, по сути два массива: один с длинами, другой с кодами. Другими словами, код (как битовая строка) хранится в ячейке памяти или регистре фиксированного размера (чаще 16, 32 или 64). Для того чтобы не произошло переполнение, мы должны быть уверены в том, что код поместится в регистр.
Оказывается, что на N-символьном алфавите максимальный размер кода может достигать (N-1) бит в длину. Иначе говоря, при N=256 (распространенный вариант) мы можем получить код в 255 бит длиной (правда для этого файл должен быть очень велик: 2.292654130570773*10^53~=2^177.259)! Ясно, что такой код в регистр не поместится и с ним нужно что-то делать.
Для начала выясним при каких условиях возникает переполнение. Пусть частота i-го символа равна i-му числу Фибоначчи. Например: A-1, B-1, C-2, D-3, E-5, F-8, G-13, H-21. Построим соответствующее дерево Хаффмана.
ROOT
/\
/ \
/ \
/\ H
/ \
/ \
/\ G
/ \
/ \
/\ F
/ \
/ \
/\ E
/ \
/ \
/\ D
/ \
/ \
/\ C
/ \
/ \
A B
Такое дерево называется вырожденным. Для того чтобы его получить частоты символов должны расти как минимум как числа Фибоначчи или еще быстрее. Хотя на практике, на реальных данных, такое дерево получить практически невозможно, его очень легко сгенерировать искусственно. В любом случае эту опасность нужно учитывать.
Эту проблему можно решить двумя приемлемыми способами. Первый из них опирается на одно из свойств канонических кодов. Дело в том, что в каноническом коде (битовой строке) не более [log2N] младших бит могут быть ненулями. Другими словами, все остальные биты можно вообще не сохранять, т.к. они всегда равны нулю. В случае N=256 нам достаточно от каждого кода сохранять лишь младшие 8 битов, подразумевая все остальные биты равными нулю. Это решает проблему, но лишь отчасти. Это значительно усложнит и замедлит как кодирование, так и декодирование. Поэтому этот способ редко применяется на практике.
Второй способ заключается в искусственном ограничении длин кодов (либо во время построения, либо после). Этот способ является общепринятым, поэтому мы остановимся на нем более подробно.
Существует два типа алгоритмов ограничивающих длины кодов. Эвристические (приблизительные) и оптимальные. Алгоритмы второго типа достаточно сложны в реализации и как правило требуют больших затрат времени и памяти, чем первые. Эффективность эвристически-ограниченного кода определяется его отклонением от оптимально-ограниченного. Чем меньше эта разница, тем лучше. Стоит отметить, что для некоторых эвристических алгоритмов эта разница очень мала ([6], [7], [8]), к тому же они очень часто генерируют оптимальный код (хотя и не гарантируют, что так будет всегда). Более того, т.к. на практике переполнение случается крайне редко (если только не поставлено очень жесткое ограничение на максимальную длину кода), при небольшом размере алфавита целесообразнее применять простые и быстрые эвристические методы.
Мы рассмотрим один достаточно простой и очень популярный эвристический алгоритм. Он нашел свое применение в таких программах как zip, gzip, pkzip, bzip2 и многих других.
Задача ограничения максимальной длины кода эквивалентна задаче ограничения высоты дерева Хаффмана. Заметим, что по построению любой нелистовой узел дерева Хаффмана имеет ровно два потомка. На каждой итерации нашего алгоритма будем уменьшать высоту дерева на 1. Итак, пусть L - максимальная длина кода (высота дерева) и требуется ограничить ее до L/ < L. Пусть далее RNi самый правый листовой узел на уровне i, а LNi - самый левый.
Начнем работу с уровня L. Переместим узел RNL на место своего родителя. Т.к. узлы идут парами нам необходимо найти место и для соседного с RNL узла. Для этого найдем ближайший к L уровень j, содержащий листовые узлы, такой, что j < (L-1). На месте LNj сформируем нелистовой узел и присоединим к нему в качестве дочерних узел LNj и оставшийся без пары узел с уровня L. Ко всем оставшимся парам узлов на уровне L применим такую же операцию. Ясно, что перераспределив таким образом узлы, мы уменьшили высоту нашего дерева на 1. Теперь она равна (L-1). Если теперь L/ < (L-1), то проделаем то же самое с уровнем (L-1) и т.д. до тех пор, пока требуемое ограничение не будет достигнуто.
Вернемся к нашему примеру, где L=5. Ограничим максимальную длину кода до L/=4.
ROOT
/\
/ \
/ \
/\ H
/ \
/ \
/ \
/ \
/ \
/ \
/\ /\
/ \ / \
/ \ / \
/ \ / \
/ \ / \
/\ /\ C E
/ \ / \
/ \ / \
/\ A D G
/ \
/ \
B F
Видно, что в нашем случае RNL=F, j=3, LNj=C. Сначала переместим узел RNL=F на место своего родителя.
ROOT
/\
/ \
/ \
/\ H
/ \
/ \
/ \
/ \
/ \
/ \
/\ /\
/ \ / \
/ \ / \
/ \ / \
/ \ / \
/\ /\ C E
/ \ / \
/ \ / \
F A D G
B (непарный узел)
Теперь на месте LNj=C сформируем нелистовой узел.
ROOT
/\
/ \
/ \
/\ H
/ \
/ \
/ \
/ \
/ \
/ \
/ \
/ \
/ \
/\ /\
/ \ / \
/ \ / \
/ \ / \
/ \ / \
/\ /\ /\ E
/ \ / \ / \
/ \ / \ / \
F A D G ? ?
B (непарный узел)
C (непарный узел)
Присоединим к сформированному узлу два непарных: B и C.
ROOT
/\
/ \
/ \
/\ H
/ \
/ \
/ \
/ \
/ \
/ \
/ \
/ \
/ \
/\ /\
/ \ / \
/ \ / \
/ \ / \
/ \ / \
/\ /\ /\ E
/ \ / \ / \
/ \ / \ / \
F A D G B C
Таким образом, мы ограничили максимальную длину кода до 4. Ясно, что изменив длины кодов, мы немного потеряли в эффективности. Так сообщение S, закодированное при помощи такого кода, будет иметь размер 92 бита, т.е. на 3 бита больше по сравнению с минимально-избыточным кодом.
Ясно, что чем сильнее мы ограничим максимальную длину кода, тем менее эффективен будет код. Выясним насколько можно ограничивать максимальную длину кода. Очевидно что не короче [log2N] бит.
Вычисление канонических кодов
Как мы уже неоднократно отмечали, длин кодов достаточно для того чтобы сгенерировать сами коды. Покажем как это можно сделать. Предположим, что мы уже вычислили длины кодов и подсчитали сколько кодов каждой длины у нас есть. Пусть L - максимальная длина кода, а Ti - количество кодов длины i.
Вычислим Si - начальное значение кода длины i, для всех i из [1..L]
SL = 0 (всегда)
SL-1 = (SL + TL) >> 1
SL-2 = (SL-1 + TL-1) >> 1
...
S1 = 1 (всегда)
Для нашего примера L = 5, T1 .. 5 = {1, 0, 2 ,3, 2}.
S5 = 00000bin = 0dec
S4 = (S5=0 + T5=2) >> 1 =
(00010bin >> 1) = 0001bin = 1dec
S3 = (S4=1 + T4=3) >> 1 =
(0100bin >> 1) = 010bin = 2dec
S2 = (S3=2 + T3=2) >> 1 =
(100bin >> 1) = 10bin = 2dec
S1 = (S2=2 + T2=0) >> 1 =
(10bin >> 1) = 1bin = 1dec
Видно, что S5, S4, S3, S1 - в точности коды символов B, A, C, H. Эти символы объединяет то, что все они стоят на первом месте, каждый на своем уровне. Другими словами, мы нашли начальное значение кода для каждой длины (или уровня).
Теперь присвоим коды остальным символам. Код первого символа на уровне i равен Si, второго Si + 1, третьего Si + 2 и т.д.
Выпишем оставшиеся коды для нашего примера:
| B = S5 = 00000bin | A = S4 = 0001bin | C = S3 = 010bin | H = S1 = 1bin |
| F = S5 + 1 = 00001bin | D = S4 + 1 = 0010bin | E = S3 + 1 = 011bin | |
| G = S4 + 2 = 0011bin |
Видно, что мы получили точно такие же коды, как если бы мы явно построили каноническое дерево Хаффмана.
Передача кодового дерева
Для того чтобы закодированное сообщение удалось декодировать, декодеру необходимо иметь такое же кодовое дерево (в той или иной форме), какое использовалось при кодировании. Поэтому вместе с закодированными данными мы вынуждены сохранять соответствующее кодовое дерево. Ясно, что чем компактнее оно будет, тем лучше.
Решить эту задачу можно несколькими способами. Самое очевидное решение - сохранить дерево в явном виде (т.е. как упорядоченное множество узлов и указателей того или иного вида). Это пожалуй самый расточительный и неэффективный способ. На практике он не используется.
Можно сохранить список частот символов (т.е. частотный словарь). С его помощью декодер без труда сможет реконструировать кодовое дерево. Хотя этот способ и менее расточителен чем предыдущий, он не является наилучшим.
Наконец, можно использовать одно из свойств канонических кодов. Как уже было отмечено ранее, канонические коды вполне определяются своими длинами. Другими словами, все что необходимо декодеру - это список длин кодов символов. Учитывая, что в среднем длину одного кода для N-символьного алфавита можно закодировать [(log2(log2N))] битами, получим очень эффективный алгоритм. На нем мы остановимся подробнее.
Предположим, что размер алфавита N=256, и мы сжимаем обыкновенный текстовый файл (ASCII). Скорее всего мы не встретим все N символов нашего алфавита в таком файле. Положим тогда длину кода отсутвующих символов равной нулю. В этом случае сохраняемый список длин кодов будет содержать достаточно большое число нулей (длин кодов отсутствующих символов) сгруппированных вместе. Каждую такую группу можно сжать при помощи так называемого группового кодирования - RLE (Run - Length - Encoding). Этот алгоритм чрезвычайно прост. Вместо последовательности из M одинаковых элементов идущих подряд, будем сохранять первый элемент этой последовательности и число его повторений, т.е. (M-1). Пример: RLE("AAAABBBCDDDDDDD")=A3 B2 C0 D6.
Более того, этот метод можно несколько расширить. Мы можем применить алгоритм RLE не только к группам нулевых длин, но и ко всем остальным. Такой способ передачи кодового дерева является общепринятым и применяется в большинстве современных реализаций.
Реализация: SHCODEC
Большинство идей, изложенных в этой статье, легли в основу программы SHCODEC (Static Huffman COder / DECoder). SHCODEC - является свободно-распространяемой программой (freeware). Программу, исходный код, документацию, а так же результаты испытаний можно найти тут: http://www.webcenter.ru/~xander
Приложение: биография Д. Хаффмана
 |
Дэвид Хаффман родился в 1925 году в штате Огайо (Ohio), США.
Хаффман получил степень бакалавра электротехники в государственном университете Огайо (Ohio State University)
в возрасте 18 лет. Затем он служил в армии офицером поддержки радара на эсминце, который помогал обезвреживать
мины в японских и китайских водах после Второй Мировой Войны. В последствии он получил степень магистра в
университете Огайо и степень доктора в Массачусетском Институте Технологий
(Massachusetts Institute of Technology - MIT).
Хотя Хаффман больше известен за разработку метода построения минимально-избыточных кодов, он так же сделал важный
вклад во множество других областей (по большей части в электронике). Он долгое время возглавлял кафедру
Компьютерных Наук в MIT. В 1974, будучи уже заслуженным профессором, он подал в отставку.
Хаффман получил ряд ценных наград. В 1999 - Медаль Ричарда Хамминга (Richard W. Hamming Medal) от Института Инженеров
Электричества и Электроники (Institute of Electrical and Electronics Engineers - IEEE) за исключительный вклад
в Теорию Информации, Медаль Louis E. Levy от Франклинского Института (Franklin Institute) за его докторскую
диссертацию о последовательно переключающихся схемах, Награду W. Wallace McDowell, Награду от Компьютерного
Сообщества IEEE, Золотую юбилейную награду за технологические новшества от IEEE в 1998.
В октябре 1999 года, в возрасте 74 лет Дэвид Хаффман скончался от рака.
|
Список литературы
[1] D.A. Huffman, "A method for the construction of minimum-redundancy codes", Proc. Inst. Radio Engineers, vol. 40, no. 9, pp. 1098-1101, Sep. 1952. [Скачать]
[2] E.S. Schwartz, B. Kallick, "Generating a canonical prefix encoding", Communications of the ACM, vol. 7, no. 3, pp. 166-169, Mar. 1964.
[3] J.V. Leeuwen, "On the construction of Huffman trees", Proc. 3rd International Colloquium on Automata, Languages, and Programming, Edinburgh University, pp. 382-410 July 1976.
[4] J. Katajainen, A. Moffat, "In-place calculation of minimum-redundancy codes", Proc. Workshop on Algorithms and Data Structures, pp. 393-402, Aug. 1995. [Скачать]
[5] A. Moffat, A. Turpin, "On the implementation of minimum-redundancy prefix codes", IEEE Transactions on Communications, vol. 45, no. 10, pp. 1200-1207, June 1997. [Скачать]
[6] R.L. Milidiu, E.S. Laber,"The warm-up algorithm: A Lagrangean construction of length restricted Huffman codes", TR-15, Departmento de Informatica, PUC-RJ, 1997. [Скачать]
[7] R.L. Milidiu, A.A. Pessoa, E.S. Laber, "Efficient implementation of the warm-up algorithm for the construction of length-restricted prefix codes", Proc. of ALENEX (International Workshop on Algorithm Engineering and Experimentation), pp. 1-17, Springer, Jan. 1999. [Скачать]
[8] R.L. Milidiu, A.A. Pessoa, E.S. Laber, "In-place length-restricted prefix coding", Proc. of SPIRE (String Processing and Information Retrieval), pp. 50-59, IEEE Computer Society, Jan. 1998. [Скачать]
[9] D.S. Hirschberg, D.A. Lelewer, "Efficient decoding of prefix codes", Communications of the ACM, vol. 33, no. 4, pp. 449-459, Apr. 1990. [Скачать]
[10] D.A. Lelewer, D.S. Hirschberg, "Data compression", Computing Surveys, vol. 19, no. 3, pp. 261-296, Sep. 1987. [Скачать]
|
Симаков Александр, Октябрь 2002 xander@online.ru |

|