Динамическое сжатие методом Хаффмана
Данная статья предполагает, что читатель знаком с принципами сжатия данных при помощи алгоритма Хаффмана. Суть алгоритма заключается в том, что символы почти любого алфавита имеют разную вероятность появления в тексте. Для примера - в русском языке буква "А" встречается намного чаще, чем "Ъ". А у Александра Сергеевича Пушкина - "Ф" - встречается всего три раза: дважды в "Сказке о царе Салтане" и один раз в "Медном всаднике". Итак, раз разные символы имеют разные вероятности появления, следовательно, если кодировать их не все по 8 бит, как они хранятся в ASCII формате, а длину кода наиболее часто встречаемых уменьшить за счёт увеличения длины кода редких символов - можно довольно неплохо сжать исходный текст. Документации по этому алгоритму в Интернете целое море и ещё небольшая лужица размером с океанчик.
Различия статической и динамической моделей Практически все существующие алгоритмы сжатия данных можно реализовать в двух вариантах - статическом и динамическом. Каждый из них имеет своё право на жизнь и, соответственно, занимает определённую нишу, используясь в тех случаях, когда он наиболее удобен. Алгоритм Хаффмана не является исключением - применяясь во многих и многих архиваторах и форматах он используется иногда в статическом (JPEG, ARJ) или в динамическом (утилита compact для UNIX, ICE) вариантах.
В чём же заключается различие между этими двумя типами реализаций? Так как алгоритм Хаффмана сжимает данные за счёт вероятностей появления символов в источнике, следовательно для того чтоб успешно что-то сжать и разжать нам потребуется знать эти самые вероятности для каждого символа. Статические алгоритмы справляются с этим делом не мудрствуя лукаво - перед тем как начать сжатие файла программа быстренько пробегается по самому файлу и подсчитывает какой символ сколько раз встречается. Затем, в соответствии с вероятностями появлений символов, строится двоичное дерево Хаффмана - откуда извлекаются соответствующие каждому символу коды разной длины. И на третьем этапе снова осуществляется проход по исходному файлу, когда каждый символ заменяется на свой древесный код. Таким образом статическому алгоритму требуется два прохода по файлу источнику, чтоб закодировать данные.
Динамический алгоритм позволяет реализовать однопроходную модель сжатия. Не зная реальных вероятностей появлений символов в исходном файле - программа постепенно изменяет двоичное дерево с каждым встречаемым символом увеличивая частоту его появления в дереве и перестраивая в связи с этим само дерево. Однако становится очевидным, что выиграв в количестве проходов по исходному файлу - мы начинаем терять в качестве сжатия, так как в статическом алгоритме частоты встречаемости символов были известны с самого начала и длины кодов этих символов были более близки к оптимальным, в то время как динамическая модель изучая источник постепенно доходит до его реальных частотных характеристик и узнаёт их лишь полностью пройдя исходный файл. Конечно, обидно, но сей недостаток можно компенсировать другим преимуществом динамического алгоритма. Так как динамическое двоичное дерево постоянно модифицируется новыми символами - нам нет необходимости запоминать их частоты заранее - при разархивировании, программа, получив из архива код символа, точно так же восстановит дерево, как она это делала при сжатии и увеличит на единичку частоту его встречаемости. Более того, нам не требуется запоминать какие символы в двоичном дереве не встречаются. Все символы которые будут добавляться в дерево и есть те, которые нам потребуются для восстановления первоначальных данных. В статическом алгоритме с этим делом немного сложнее - в самом начале сжатого файла требуется хранить информацию о встречаемых в файле источнике символах и их вероятностных частотах. Это обусловлено тем, что ещё до начала разархивирования нам необходимо знать какие символы будут встречаться и каков будет их код.
Ниже представлены алгоритмы работы статического и динамического архиваторов кодами Хаффмана.
Статический алгоритм:
InitTree ' Инициализируем двоичное дерево For i=0 to Ubound(CharCount) CharCount(i)=0 ' Инициализируем массив частот элементов алфавита Next Do While not EOF(Файл источник) ' Запускаем первый проход файла Get Файл источник, C ' Читаем текущий символ CharCount(C)= CharCount(C)+1 ' Увеличиваем на один частоту его встречаемости Loop ReBuildTree ' По полученным частотам строим двоичное дерево WriteTree (Файл приёмник) ' Записываем в файл двоичное дерево Do While not EOF(Файл источник) ' Запускаем второй проход файла Get Файл источник, C ' Читаем текущий символ code=FindCodeInTree(C) ' Находим соответствующий ему код в дереве Put Файл приёмник, code ' Записываем последовательность бит в файл Loop Процедура InitTree инициализирует двоичное дерево, обнуляя значения, веса, и указатели на родителя и потомков текущего листа. Далее выполняется первый проход по источнику данных с целью проверки частотности символов - результаты которого запоминаются в массив CharCount. Размерность этого массива должна равняться количеству элементов алфавита источника. В общем случае, для сжатия произвольного компьютерного файла, его длина должна составлять 256 элементов. Затем, в соответствии с полученным набором частот строим двоичное дерево ReBuildTree. Во время второго прохода, перекодируем источник в соответствии с деревом и записываем получаемые последовательности бит в сжатый файл. Для того, чтоб потом возможно было восстановить сжатые данные - необходимо, также, в полученный файл, сохранить копию двоичного дерева WriteTree.
Динамический алгоритм:
InitTree ' Инициализируем двоичное дерево For i=0 to Ubound(CharCount) CharCount(i)=0 ' Инициализируем массив частот элементов алфавита Next Do While not EOF(Файл источник) ' Запускаем проход файла Get Файл источник, C ' Читаем текущий символ If C нет в дереве then ' Проверяем встречался ли текущий символ раньше code=Код "пустого" символа & Asc(C) ' Если нет, то запоминаем код пустого листа и ASCII код текущего символа else code=Код C ' Иначе запоминаем код текущего символа End if Put Файл приёмник, code ' Записываем последовательность бит в файл ReBuildTree(С) ' Обновляем двоичное дерево символом Loop Динамическое сжатие использует более гибкий подход. Первоначально двоичное дерево кодов является пустым и процедура InitTree записывает только лист содержащий "пустой" символ. Затем кодируется и записывается в сжатый файл поступивший на вход текущий символ. Процедура ReBuildTree обновляет дерево в соответствии с этим символом. Символы добавляются в словарь только по мере их появления в файле источнике. Если появившийся символ раньше не встречался, то выводим в поток код "пустого" символа, то есть символа, который раньше не встречался, а затем ASCII код самого символа, который гарантирует нам, что при разархивировании восстанавливаемая информация не сможет двояко трактоваться.
Динамический алгоритм сжатия Хаффмана Динамическое сжатие методом Хаффмана было предложено независимо Фоллером [1973] и Галлагером [1978]. В 1985 Дональд Кнут разработал окончательный усовершенствованный вариант алгоритма - вследствие чего алгоритм получил название FGK (Faller, Gallager, Knuth) алгоритма. Основным принципом FGK алгоритма - является свойство "братства". Двоичное дерево обладает данным свойством, если каждый его узел (за исключением корневого) имеет в дереве узла "брата" и, при расположении всех узлов в списке, в порядке неувеличения их весов, узлы "братья" находятся по соседству. "Братьями" назовём два узла, которые имеют общего родителя.
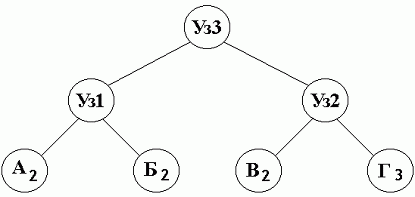
Например, для указанного дерева, при выписывании узлов в требуемый список - получаем:
Уз3 Уз2 Уз1 Г В Б А 9 5 4 3 2 2 2 Где верхний ряд означает узел дерева, а нижний его вес. Таким образом выясняем, что данное дерево обладает свойством "братства", так как каждый, кроме корневого, узел имеет "брата" и все узлы "братья" находятся в списке по соседству { А - Б }, { В - Г }, { Уз1 - Уз2 }. Листья такого дерева представляют собой символы извлекаемые из исходного файла, а веса листьев - количество появлений этих символов в исходном файле. По мере прохождения алгоритма через файл веса листьев могут либо увеличиваться, либо оставаться без изменений.
Первоначально дерево состоит из одного "пустого" узла. Этот узел является единственным листом, который не содержит никакого символа и имеет нулевой вес. Он предназначается для кодирования тех символов, которые ранее не попадали во входной поток. Далее, по мере поступления на вход программы архиватора символов из исходного файла, проверяется, есть ли уже такой символ в дереве или нет. Если символ присутствует - его код передаётся сжатому файлу, затем его (и всех его родителей) вес инкрементируется и дерево пересчитывается по новой. При отсутствии символа в дереве - в сжатый файл передаётся код "пустого" символа, следующие за которым биты содержат информацию однозначно определяющий новый символ (чаще всего это ASCII код). После чего в дерево добавляется ещё один лист, который содержит новый символ и имеет вес 1. Инкрементируются веса всех родителей новоиспечённого узла. Снова пересчитываем дерево.
Так как "пустой" узел имеет вес 0, то при пересчёте дерева он всегда будет иметь самый длинный код. Следовательно, каждый появившийся новый символ будет иметь код равный по длине коду "пустого" узла или меньший его на 1 бит. Благодаря чему самые редковстречаемые символы, которые будут, соответственно, позже появляться - будут иметь самые длинные коды - что полностью соответствует принципам алгоритма сжатия Хаффмана.
Принципы построения основных процедур В соответствии с описанным выше алгоритмом сжатия методом Хаффмана можно выделить три основные процедуры от алгоритмов реализации которых зависят характеристики (производительность, коэффициент сжатия и т.д.) программы сжатия. Процедура InitTree - инициализирующая двоичное дерево, процедура добавления нового символа в дерево и процедура ReBuildTree - модифицирующая текущее дерево в соответствии с новой поступившей информацией. Рассмотрим принципы их реализации в обратном порядке.
От процедуры ReBuildTree во многом зависит быстродействие программы архиватора, так как именно она должна после каждого поступившего символа заново перестраивать двоичное дерево кодов. Самый простой и надёжный способ - конечно же полное построение дерева - однако в этом случае алгоритм будет настолько медленным, что при архивации даже самого маленького файла можно будет успеть выпить пару чашек кофе и немножко вздремнуть. Полное построение двоичного дерева - довольно большая и нелёгкая работа даже для современных компьютеров. Но выход всё-таки есть! Вспомним, что мы пользуемся для сжатия данных FGK алгоритмом, который обладает свойством "братства". Согласно правилам, при расположении всех узлов в списке, в порядке неувеличения их весов, узлы "братья" находятся по соседству. Откуда следует, что вместо того, чтоб постоянно полностью модифицировать всё дерево можно хранить его в виде упорядоченного списка и изменять только те элементы списка, которые требуют изменения.
Для рассмотренного выше дерева упорядоченный список представлял собой:
Уз3 Уз2 Уз1 Г В Б А 9 5 4 3 2 2 2 Теперь, если очередным символом во входящем потоке будет символ "Г", тогда увеличиваем его вес на 1. Очевидно, что вес родителя Уз2 теперь не соответствует сумме весов потомков, поэтому его тоже следует инкрементировать. Увеличив вес узла Уз2 - переходим к его родителю - корню дерева Уз3, вес которого так же увеличивается на 1. Новый список теперь будет иметь вид:
Уз3 Уз2 Уз1 Г В Б А 10 6 4 4 2 2 2 А дерево соответственно станет:
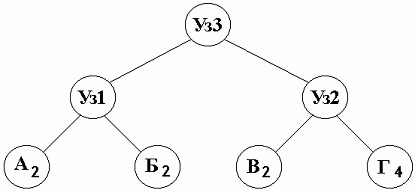
Нам потребовалось всего три действия, чтоб изменить дерево. В общем случае необходимо увеличить на 1 вес листа поступившего на вход символа, а затем инкрементировать веса всех его родителей вплоть до корня дерева. То есть среднее число операций будет равняться среднему количеству битов (или средней длине пути от листа к корню дерева), необходимых для того, чтоб закодировать символ.
Однако возможен вариант, когда упорядоченность списка нарушается. Например, если для полученного дерева следующий символ снова будет "Г", и мы просто увеличим веса, тогда после их кодирования список примет вид:
Уз3 Уз2 Уз1 Г В Б А 11 7 4 5 2 2 2 Как видно свойство упорядоченности нарушено. Символ "Г" вес которого больше чем вес Уз1 стоит раньше него в списке. В таком случае необходимо произвести операцию упорядочивания списка. Для этого после инкрементации веса символа начинаем двигаться по списку, в сторону увеличения веса, до тех пор пока не найдем последний узел с меньшим весом чем текущий. Затем переставляем текущий и найденный узлы восстанавливая таким образом порядок в списке. При этом родители обоих узлов тоже изменяются. Родителем текущего узла становится родитель найденного и наоборот. Дальше увеличивается вес нового родителя и так далее, до самого корня дерева. Новый список уже будет выглядеть следующим образом:
Уз3 Уз2 Г Уз1 В Б А 10 6 5 4 2 2 2 А дерево соответственно:
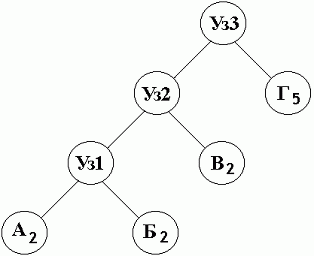
Из приведённого примера видно, что чем чаще встречается тот либо иной символ, тем ближе он находится к началу списка и короче код имеет. В последнем двоичном дереве самый часто встречаемый символ "Г" имеет самый короткий код - 1 бит.
В общем виде алгоритм модификации дерева можно записать так:
Public Sub ReBuildTree (Символ as Byte) ТекущийУзел = ЛистСоответствующий(Символ) ' Находим в дереве лист соответствующий символу Do While True ТекущийУзел.Вес=ТекущийУзел.Вес + 1 ' Увеличиваем его вес на 1 If ТекущийУзел=КореньДерева then ' Является ли текущий узел корнем дерева Exit Do ' Если да, то заканчиваем процедуру обновления else if ТекущийУзел.Вес > (ТекущийУзел+1).Вес ' Проверяем не нарушена ли упорядоченность i=1 Do WhileТекущийУзел.Вес > (ТекущийУзел+i).Вес i=i+1 Loop Перестановка ТекущийУзел, ТекущийУзел+i ' Если упорядоченность нарушена, то восстанавливаем её путём обмена узлов End if ТекущийУзел = ТекущийУзел.Родитель ' Переходим к родителю текущего узла End if Loop End sub Теперь, после того как стали ясны принципы построения и модификации двоичного дерева, возникает вопрос о добавлении в дерево нового символа. Согласно алгоритму, при появлении во входном потоке нового символа в файл архив выдаётся код "пустого" символа, а затем последовательность бит однозначно идентифицирующих новый символ.
Процедура добавления нового символа состоит в том, что в хвост упорядоченного списка, коим является наше дерево кодов, добавляются два новых элемента - первый из них становится листом для нового символа, а второй дополнительным узлом. Только что созданный дополнительный узел берёт на себя родителя "пустого" символа и сам становится родителем для нового и "пустого" символов. Дополнительный узел необходим, так как общее количество узлов дерева должно быть равным количеству листьев -1.
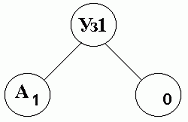
Уз1 А 1 1 0 Например, при имеющемся двоичном дереве с одним символом "А" и нулевым узлом, если следующим символом поступающим из файла источника является "Б" необходимо добавить его в список.
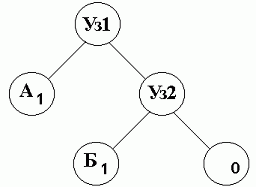
Уз1 А Уз2 Б 2 1 1 1 0 Первоначально веса нового символа и его родительского узла устанавливаются равными 0, однако в конце процедуры добавления символа идёт обращение к процедуре построения дерева ReBuildTree, где указывается только что созданный символ. ReBuildTree увеличивает на один вес символа, а так же его родителей в дереве и перемещает их (если это необходимо) согласно алгоритму по списку так, чтоб сохранялись принципы упорядоченности списка, и не нарушалось построение двоичного дерева.
Public Sub AddNode (Символ as Byte) Создать(НовыйУзел) ' Создаём новый узел дерева Создать(НовыйЛист) ' Создаём новый лист дерева (для символа) НовыйУзел.Родитель=ПустойЛист.Родитель ' Родителем нового узла делаем родителя пустого символа ПустойЛист.Родитель=НовыйУзел ' Делаем новый узел родителем пустого НовыйЛист.Родитель=НовыйУзел ' Делаем новый узел родителем нового листа НовыйУзел.Вес=0 ' Присваиваем новому узлу нулевой вес НовыйЛист.Вес=0 ' Присваиваем новому листу нулевой вес НовыйЛист.Символ=Символ ' Запоминаем в листе символ, ради которого его создавали ReBuildTree(Символ) ' Обновляем двоичное дерево End Sub Инициализация дерева, процедура InitTree, представляет собой ни что иное, как просто создание "пустого" символа. В самом начале упорядоченного списка. Так как при начале кодирования дерево не содержит ни одного символа, то "пустой" символ не смотря на свой нулевой вес будет первым и единственным и при обращении к нему выдаст в поток однобитный код 0.
Заключение Статическое кодирование Хаффмана довольно широко применяется в современных алгоритмах сжатия, но не в чистом виде, а как одна из ступеней сжатия в более сложных алгоритмах. Динамический же вариант алгоритма на практике, в последнее время, уступил более гибким и скоростным алгоритмам и применяется в основном только в экспериментальных целях.
наверх