М.А. Смирнов
Обзор применения методов безущербного сжатия данных в СУБД
Часть 3
Содержание | Часть 1 | Часть 2 | Часть 3 | Часть 4

Сжатие индексных структур

Основные типы индексов

В настоящее время основными типами индексных структур, используемых в РСУБД, являются B-деревья (B-tree) и битовые карты (bitmap), иначе называемые битовыми индексами [26, 28, 54]. Также применяются:

  • проективные индексы (projection index) [26];

  • R-деревья (R-tree) для многомерных данных [24];

  • датаиндексы (DataIndex) [26].

Число же экспериментальных схем равно, видимо, нескольким десяткам [28].

Наибольшее внимание в публикациях уделяется вопросу экономного кодирования битовых карт. Интерес объясняется тем, что данный тип индексов обычно позволяет выполнять запросы существенно быстрее, чем индексы других известных типов [26, 33]. Но размер индексной структуры получается очень большим, если мощность множества значений индексируемых атрибутов велика.

В самом простом случае организации битовой карты каждой строке таблицы ставится в соответствие битовый вектор, состояние которого определяется значением индексируемого атрибута. -ый бит принимает значение 1 для некоторой строки, если соответствующий атрибут этой строки имеет -ое значение из множества всех значений атрибута. Например, если индексируется столбец “Пол”, и область значений равна , то битовый вектор будет принимать значения:

  • для строк со значением атрибута “Пол” = “мужской”;

для строк со значением атрибута “Пол” = “женский”.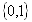

Только один бит вектора может быть единичным. Длина битового вектора равна битам, где — мощность множества значений индексируемого атрибута.

Существуют другие разновидности битовых индексов [13, 54, 55]. Так называемые односторонние битовые индексы характеризуют результат одностороннего сравнения “<”, а не точного “=”. Битовые вектора в этом случае состоят из одной последовательности единиц и одной последовательности нулей. Также разработаны битовые индексы для двухстороннего сравнения. Битовые вектора для одностороннего сравнения имеют длину битов, для двухстороннего — битов. Таким образом, проблема экономного представления индексов этих разновидностей также актуальна.

Сжатие битовых карт

В литературе обозначено два подхода к решению проблемы уменьшения размера битовых карт:

  • декомпозиция, использование набора битовых карт [13, 33];

  • сжатие собственно битовых карт [13, 33, 55].

Кроме уменьшения требуемого пространства для хранения, сжатие может обеспечить повышение скорости выполнения запросов. Это обуславливается следующим:

  • уменьшается число операций обращения к внешней памяти;

  • ряд булевых операций может быть выполнен непосредственно над сжатыми данными, причем быстрее, чем над незакодированными.

В [33] произведено сравнение четырех алгоритмов сжатия битовых карт:

  1. реализация LZH в библиотеке zlib, использующей тот же формат сжатых данных Deflate, что и компрессор Gzip;

  2. сжатие посредством zlib с предварительным кодированием длин серий (LZH+RLE);

  3. код переменной длины, задаваемый алгоритмом ExpGol, два варианта;

  4. код переменной длины, задаваемый алгоритмом байтового сжатия битовых карт (БСБК) — Byte-Aligned Bitmap Codes, два варианта [5].

Код ExpGol является расширением -кода Элайеса11 для представления целых чисел. Пусть — это набор целых чисел . При кодировании необходимо найти такое , что

.

Пусть

.

Тогда кодовое слово для состоит из кодового слова для и числа , записанного с помощью битов. Для представления может быть использован тот же -кода Элайеса: нулевых битов, за которыми следует единичный бит. Например, числам при использовании -кода12 соответствуют слова . Для эффективного кодирования последовательности нулей используется

.

Параметр выбирается равным медиане распределения длин серий нулей для первого варианта кода ExpGol и геометрического среднему — для второго.

Код БСБК обеспечивает высокую скорость кодирования-декодирования, поскольку все действия производятся над последовательностями байтов. Булевские операции над битовыми индексами, закодированными посредством БСБК, могут выполняться существенно быстрее, чем над незакодированными.

Код БСБК может быть односторонним и двухсторонним. Односторонний код позволяет кодировать серии нулей, а двухсторонний — как нулей, так и единиц. Каждое кодовое слово одностороннего кода состоит из двух частей:

  • “окно” (gap);

  • окончание (ending).

Содержимое “окна” определяет, сколько нулевых байтов предшествует окончанию. Окончание может содержать последовательность незакодированных байтов или специальный контрольный байт. Используется ряд приемов для экономного кодирования размеров “окна” и окончания. Таким образом, БСБК есть разновидность байт-ориентированного кодирования длин серий.

В [33] указывается, что алгоритм LZH+RLE не продемонстрировал ни разу лучшего сжатия, поэтому его характеристики не приводятся. Было установлено, что степень сжатия ExpGol для двух вышеописанных вариантов выбора практически не отличается. Поэтому характеристики варианта кода при вычислении по геометрическому среднему также были опущены. В сравнении были использованы как односторонний код БСБК, так и двухсторонний. Из приводимых результатов сравнений для сгенерированных и реальных индексных данных следует:

  • наибольшая степень сжатия для “густых” битовых карт с относительно большим количеством единиц обеспечивается LZH; в случае кластеризации серий нулей и единиц преимущество может иметь двухсторонний БСБК;

  • наибольшую степень сжатия для разреженных битовых карт с вероятностью появления единицы дает ExpGol; например, при 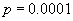степень сжатия для ExpGol в три раза выше, чем у LZH;

  • бо́льшую скорость выполнения операций с индексами для “густых” битовых карт обеспечивает LZH;

  • наибольшую скорость выполнения операций с индексами для разреженных битовых карт дает использование БСБК.

Необходимо отметить, что формат Deflate, в соответствии с которым реализована библиотека сжатия zlib, налагает ограничение на длину кодируемой за один шаг строки (длину совпадения) [1]. Этот порог равен 258 битам, что в данных условиях является жестким ограничением и неизбежно должно ухудшать степень сжатия сильно разреженных битовых карт.

В диссертационной работе [54] рассмотрены ряд проблем использования битовых индексов для поддержки сложных многомерных запросов к научным данным, содержащим большое количество недискретных атрибутов, в первую очередь чисел с плавающей запятой. При этом изучены вопросы сжатия соответствующих модификаций битовых карт. В частности, применительно к решаемой задаче исследован вариант двухстороннего БСБК. Приводятся результаты ряда экспериментов, указывающие на ускорение выполнения запросов некоторых типов при использовании сжатых индексов.

В работах [59, 60] предложена схема сжатия на основе кодирования длин серий, обеспечивающая бо́льшую скорость выполнения операций с индексами, чем БСБК. Метод назван авторами “пословное гибридное кодирование длин серий” (Word-Aligned Hybrid run-length code, WAH). Название определено тем, что закодированные данные группируются в машинные слова, а не в байты, как в БСБК. Соответственно, вся обработка может выполняться на уровне слов. Определены два типа слов: заполнители (“fill words”) и литералы. Слова различаются значением старшего бита. В слове-заполнителе указывается значение бита, образующего серию, и длина серии таких одинаковых значений. В литералах сохраняются в исходном виде те биты, которые не удалось сжать с помощью заполнителей. Требуется, чтобы длина серии, кодируемой заполнителем, была кратной числу рабочих битов литерала. Например, если машинное слово состоит из 32 битов, то длины совпадений должны быть кратны 31.

Результаты сравнительных экспериментов, приведенные в [60], свидетельствуют о 12-кратном превосходстве в скорости выполнения запросов при использовании предложенной схемы пословного кодирования относительно сжатия с помощью БСБК. Размер индексной структуры при этом на 60% больше размера структуры для БСБК. Для тестирования была использована таблица с данными результатов физических экспериментов, содержащая порядка 2.2 миллиона записей. Отмечается, что при вероятности появления в битовой карте единицы размер индекса для предложенного метода примерно в 2.5 раза превышает размер индекса для БСБК.

Следует отметить, что основной проблемой всех способов сжатия битовых индексов, основанных на кодировании длин серий, является решение задачи эффективного декодирования с произвольным доступом.

Экономное кодирование B-деревьев

Сжатие индексных данных в B-дереве позволяет не только уменьшить размер структуры, но и приводит к получению более “плоского” дерева, т.е. с меньшей высотой. Это ускоряет доступ к отдельному ключу.

Обеспечение возможности непосредственного сравнения сжатых данных требует использования алгоритмов кодирования с сохранением упорядоченности. В [24] указано, что для сжатия вершин B-дерева может быть использован предложенный вариант метода упаковки битов, названный “сжатие кадра ссылок”. Эта модификация была рассмотрена выше в подпункте “Упаковка битов” пункта “Кодирование числовых данных”. Как и обычный метод упаковки битов, данный вариант сохраняет порядок сортировки, но годен только для кодирования целых чисел. Универсальная схема сжатия с сохранением упорядоченности описана в работе [6]. Алгоритм является словарным и в этом сходен с предложенной в [61] схемой модификации LZW для сохранения упорядоченности. Но он обеспечивает бо́льшую степень сжатия. В статье указано, что предложенный алгоритм позволил сжать реальные индексные данные в 5 раз.

Сжатие индексов других типов

Вопрос экономного кодирования R-деревьев обсуждается в [24, 25]. Для сжатия таких структур предлагается использовать схему “сжатие кадра ссылок”, основанную на методе упаковки битов и рассмотренную выше в подпункте “Упаковка битов” пункта “Кодирование числовых данных”.

Схемы сжатия датаиндексов изучены в [26, 27]. Экономное кодирование индексных данных выполнялось на уровне страницы. Наилучшие результаты с точки зрения степени сжатия были получены для LZW с предварительным взятием разности значений (дифференциальным кодированием).

Сжатие результирующих наборов

Сжатие результирующих наборов, получаемых в итоге выполнения запросов, актуально в силу ряда причин:

  • уменьшается время передачи результата клиенту, что особенно значимо при низкой пропускной способности канала связи (например, радиоканала);

  • экономится память клиентского вычислительного устройства, которая в случае карманных компьютеров может иметь малый объем и являться критическим ресурсом;

  • уменьшается время обмена информацией при выполнении запроса к распределенной системе, когда запрос разбивается на подзапросы, выполняемые на различных компьютерах.

Как уже отмечалось, вопросу сжатия результирующих наборов в литературе уделяется недостаточно внимания.

В [14, 16] предложена общая схема сжатия результирующих наборов, учитывающая вопросы выбора совокупности методов сжатия для кодирования набора на основании статистической и семантической информации. Последнее включает знание ограничений целостности в БД и запроса как такового. Например, учет упорядоченности по некоторым столбцам.

Введено понятие “плана сжатия” результата (“compression plan”), состоящего из совокупности “операторов сжатия”. Каждый оператор сжатия соответствует применению определенного алгоритма экономного кодирования к фрагменту результирующего набора. В общем случае фрагмент уже может быть сжат за счет использования нескольких операторов. Для упрощения анализа в [14] фрагмент принят равным одному или нескольким столбцам. Оператор сжатия определяется как , где  — набор сжимаемых столбцов,  — входная гранулярность, определяющая минимальный блок данных, который может быть сжат посредством ,  — выходная гранулярность,  — алгоритм сжатия,  — требуемый тип входных данных,  — тип выходных данных. План сжатия определен как , где  — сжимаемый набор данных. В общем случае изменение порядка применения операторов дает иной план. В зависимости от типа операторов и их взаимозависимостей план может выполняться в параллельном и конвейерном режимах. Например, параллельно могут применяться операторы, кодирующие разные колонки таблицы.

Эффективность экономного кодирования определяется выбором плана сжатия, оптимального или достаточно хорошего по заданному критерию. В [14] использован следующий вид критерия стоимости плана:

,

где  — перенастраиваемые константы, задающие значимость соответствующих затрат;

 — цена кодирования;

 — цена декодирования;

 — экономия пропускной способности канала связи;

 — экономия памяти клиентского вычислительного устройства.

При поиске удовлетворительного плана сжатия также должно обеспечиваться согласование типа и гранулярности входных и выходных данных операторов. Например, оператор, применяемый к значению атрибута, не может быть использован после оператора, сжимающего на уровне строки. Кроме того, налагается ограничение, что каждый оператор может только один раз войти в план.

Исчерпывающий алгоритм поиска наилучшего плана, состоящий в переборе всех вариантов, является конечным, поскольку конечно множество операторов, и каждый из них может быть использован только один раз. Но временна́я сложность алгоритма экспоненциально зависит от количества сжимаемых фрагментов. Если, как принято в работе, фрагмент состоит целиком из одного или нескольких столбцов, то это количество столбцов. Поэтому предложен практически ценный субоптимальный эвристический алгоритм, временная сложность которого на практике близка к , где  — количество атрибутов в наборе.

Для проведения экспериментов в работе были использованы несколько алгоритмов:

  • нормализация и группировка отсортированных данных;

  • упаковка битов через кодирование разницы между текущим значением атрибута и нижней границей его диапазона значений;

  • кодирование по полуадаптивному словарю значений атрибута;

  • дифференциальное кодирование;

  • LZH-сжатие (применялся компрессор WinZip);

  • устранение ведущих нулей чисел, а также ведущих и оконечных пробелов строк;

  • кодирование по Хаффману;

  • арифметическое сжатие.

Схемы нормализации и группировки отсортированных данных предложены в этой же работе. Нормализация отсортированных данных предполагает устранение из набора значений атрибутов, которые находятся в известной функциональной зависимости от известных значений других атрибутов. Например, пусть результирующий набор был получен слиянием двух таблиц и с атрибутами и соответственно, при этом является первичным ключом в . Тогда можно определить , зная . Если результат отсортирован по , то набор на Рис. 4 может быть без потери информации представлен в виде Рис. 5. Схема группировки отсортированных данных аналогична, но позволяет устранить дублирование значений только тех столбцов, по которым отсортирован набор.

Рис. 4. Результирующий набор без сжатия

Рис. 5. Результирующий набор после нормализации отсортированных данных

Выбор алгоритма при формировании плана сжатия определялся статистической и семантической информацией, известной после оптимизации плана выполнения запроса (т.е. до собственно выполнения запроса). Результаты экспериментов, проведенные с использованием запросов теста TPC-D, свидетельствуют о возможности многократно — в 2 и более раз — улучшить сжатие за счет выбора хорошего плана сжатия, учитывающего семантическую информацию о данных. Также отмечается ускорение передачи данных с учетом времени кодирования и декодирования, если пропускная способность канала составляет менее 500 кБайт/с, а клиентское устройство представляет собой типовой персональный компьютер. Если клиентское вычислительное устройство является “карманным” компьютером, то это требует применения более простых методов сжатия, с тем чтобы декодирование выполнялось с меньшими затратами процессорного времени и памяти. Указывается, что применение сжатия результирующих наборов в этом случае позволило в 2 раза уменьшить расход памяти клиентского “карманного” компьютера при замедлении доступа к данным только на 15%.

Исследования, описанные в [14], при всей своей ценности не исчерпывают вопрос сжатия результирующих наборов. Он требует более полной и детальной проработки.

Сходные области исследований: сжатие данных в информационно-поисковых системах

Информационно-поисковые системы основаны на использовании текстовых баз данных. Создание таких систем связано типичными проблемами практической реализуемости и производительности, разрешение которых требует применения методов экономного кодирования данных.

Информационно-поисковая система должна в ответ на текстовый запрос выдавать набор документов (текстов), отсортированный по уменьшению предполагаемого соответствия документа запросу. Обычно запрос представляет собой совокупность слов, которые должны встречаться в требуемом тексте.

Типовая схема реализации хранения данных предполагает экономное представление как собственно документов, так и индексных структур, обеспечивающих быстрый анализ соответствия документа и доступ к нему [9, 38, 39]. В качестве основной схемы индексирования используется так называемый словоуказатель, или инвертированный файл (inverted file). Словоуказатель позволяет найти для заданного слова все тексты, в которых оно встречается. Каждая запись словоуказателя соответствует одному слову из всего множество слов, употребляющихся в индексируемых документах. Запись состоит из набора идентификаторов текстов, в которых встречается слово, и частот встречаемости. Запись также включает ссылку на слово в словаре уникальных слов или само слово. Словарь может представляться в виде обычного массива или некоторой структуры с индексированием, например B-дерева [39]. Отображение идентификаторов документов в их физические адреса выполняется с помощью таблицы. Задача экономного представления словоуказателя аналогична проблеме сжатия индексных структур в обычных СУБД. Для кодирования словоуказателя применялись как методы сжатия битовых карт, например код Голомба [38], так и методы кодирования целых чисел, в частности коды Элайеса [9].

Сжатие собственно текстов исследователи предлагали выполнять путем полуадаптивного кодирования на уровне слов. В этом случае общая для всей БД модель дает возможность независимого декодирования отдельного текста, и обеспечивается бо́льшая скорость декодирования, чем при посимвольном сжатии. Например, в [38] для сжатия текстов предложен полуадаптивный алгоритм Хаффмана.

Таким образом, вопросы применения сжатия данных в информационно-поисковых системах аналогичны возникающим при экономном кодировании баз данных произвольного вида, содержащих редко изменяющуюся, статическую информацию.

Оптимизация запросов в СУБД со сжатием данных

Использование сжатия данных требует соответствующей переработки подсистемы оптимизации плана выполнения запросов и, возможно, изменения алгоритмов оптимизации. Это объясняется высокой вычислительной стоимостью операций декодирования и кодирования.

В работах [14, 15] произведен анализ проблемы и предложен вариант решения. Рассмотрены несколько стратегий выполнения декодирования при отработке запросов к БД.

  1. “Жадное” декодирование, при котором данные разжимаются при их передаче в основную память. “Жадное” декодирование предлагается в ранних работах по сжатию в СУБД, например, в [32]. Преимущество жадного декодирования в локализации изменения программного кода, обеспечивающего работу со сжатой БД, на уровне модуля управления памятью. Такая стратегия является естественной, если предполагается аппаратная реализация сжатия. Но при “жадном” декодировании генерируются субоптимальные планы выполнения запросов, поскольку не учитывается возможность выполнения непосредственно над сжатыми данными таких операций, как, например, проецирование и объединение по эквивалентности [29]. На практике таблицы БД уровня предприятия часто содержат сотни колонок, но большинство запросов задействуют всего несколько. “Жадное” декодирование в таких случаях крайне неэффективно.

  2. “Ленивое” декодирование предполагает, что данные остаются сжатыми в течение выполнения запроса до тех пор, пока это допустимо, а декодируются только при необходимости, после чего остаются разжатыми на выходе. Такой подход является более эффективным. Однако использование этой стратегии может привести к увеличению размера промежуточных наборов, поскольку данные остаются разжатыми на выходе. В результате может увеличиться число операций ввода-вывода при выполнении последующих действий плана запроса.

  3. “Вре́менное” (transient) декодирование, предложенное в [14], позволяет избежать увеличения размеров промежуточных результатов. При использовании данной стратегии реляционные операторы модифицируются так, чтобы временно разжимать данные, если это необходимо для выполнения операции, но оставлять их на выходе сжатыми. Такие операторы, получающие и возвращающие сжатые данные, автор подхода называет “вре́менными” операторами. При использовании временного оператора данные, находящиеся в буферном пуле, всегда остаются сжатыми. Разжатое значение сохраняется во временной программной переменной и “забывается” сразу после использования.

В рамках реализации стратегии “временного” декодирования в [14] предложены методы нахождения оптимального и субоптимального плана выполнения запроса в СУБД со сжатием данным. Дана оценка сложности алгоритма определения оптимального плана. Сложность по машинной памяти составляет , где  — число отношений в запросе, — число атрибутов, требующих декодирования (либо для выполнения операций, либо для формирования результирующего набора). Сложность по времени равна . При этом для типового оптимизатора сложность по машинной памяти составляет , сложность по времени — . Для предложенного эвристического субоптимального алгоритма поиска, обеспечивающего высокую скорость обработки, сложность по машинной памяти равна , где  — наибольшее число анализируемых планов с наименьшей ценой выполнения, сложность по времени — . Экспериментально показана эффективность решений. План, выбираемый по субоптимальному алгоритму, для всех тестов совпал с оптимальным при . Использование субоптимального алгоритма в сочетании с “временным” декодированием позволило в 2-10 раз увеличить скорость выполнения запросов и сэкономить до 50% от объема буферного пула.

В работе [4] предлагается алгоритм оптимизации плана вычисления булевских выражений, выполняемых с использованием сжатых битовых индексов. Из результатов расчетов могут быть определены наилучший формат представления битового индекса и способ выполнения заданной булевской операции. Алгоритм основан на динамическом программировании и имеет линейную сложность по времени. Используется модель стоимости выполнения операций на основе оценок разреженности битовой карты и скорости выполнения действий для конкретного формата представления битового индекса. Отмечается увеличение скорости выполнения запросов на десятки процентов вплоть до нескольких раз в случае использования схем сжатия битовых индексов БСБК и ExpGol. Максимальные улучшения зафиксированы в тех случаях, когда индексированные атрибуты имеют высокую мощность множества значений.

Проблема оптимизации плана выполнения запроса при использовании экономного кодирования также затронута в [57]. Предложен достаточно простой вариант модификации стандартной подсистемы оптимизации посредством:

  • добавления оценок стоимости декодирования полей записи в модель стоимости операций;

  • изменения оценок стоимости операций обмена с оперативной памятью и внешней памятью, поскольку они ниже при использовании сжатия; предлагается эмпирический коэффициент пересчета 0.5;

  • обеспечения возможности сжатия промежуточных результатов, если они сохраняются во внешней памяти.

Результаты исследований показывают, что задача разработки адекватной системы оптимизации плана выполнения запроса является ключевой для СУБД со сжатием данных.

Выводы

Методы сжатия, предлагаемые к использованию в СУБД, обычно представляют собой разновидности кодирования длин серий и словарного сжатия, обеспечивающие быстрое декодирование. Во многих схемах учет сильных вертикальных связей между значениями колонок учитывается с помощью предварительного дифференциального кодирования. Практически не применяются сложные статистические методы. Слабо исследованы возможности автоматического распознавания и учета структуры данных. Сходные подходы применяются только для сжатия с потерями информации.

Обычно приводимые оценки степени сжатия баз данных составляют 2..5 раз, часто отмечается ускорение выполнения запросов за счет сжатия на несколько десятков процентов и больше. Но объективное сравнение различных способов экономного кодирования затруднено, поскольку нечасто приводятся характеристики реализаций для стандартных тестовых баз данных. Отсутствие общепризнанных эталонов является большой проблемой само по себе.

В области экономного кодирования индексов основной интерес для исследователей имеет поиск формата битовых индексов, который бы обеспечил наибольшую производительность при выполнении запросов.

Задача экономного представления результатов набора практически не рассматривается в литературе.

Проблеме оптимизации планов выполнения запросов при использовании сжатия только в последнее время стало уделяться должное внимание. Известные результаты свидетельствуют о возможности повышения производительности СУБД на десятки процентов и более за счет изменения оптимизатора и алгоритма выполнения реляционных операторов.

Также следует отметить недостаточную активность в создании и внедрении методов сжатия, позволяющих оперировать при выполнении запросов непосредственно закодированными данными. Существующие разработки ориентированы на кодирование индексных данных.

Содержание | Часть 1 | Часть 2 | Часть 3 | Часть 4

 

Подстрочные примечания

11 Elias P. Universal codeword sets and representations of the integers. IEEE Transaction on Information Theory, 21(2):194-203, Mar. 1975.
12 Строго говоря, в соответствии с обозначениями в исходной статье Элайеса это не -код, а '-код (гамма-штрих код).