М.А. Смирнов
Обзор применения методов безущербного сжатия данных в СУБД
Часть 2
Содержание | Часть 1 | Часть 2 | Часть 3 | Часть 4

Сжатие табличных данных

Для табличных данных характерны следующие типы избыточности, которые обычно проявляются одновременно [49]:

• разница в частоте встречаемости отдельных символов (элементов); например, если поле текстовое, то число пробелов обычно значительно превышает количество любых других символов;
• наличие последовательностей одинаковых символов; например, это могут быть серии отсутствующих значений или нулей, а также серии пробелов, дополняющие значения строкового типа до получения максимальной ширины, принятой для колонки; последний пример характерен для СУБД, не поддерживающих переменную длину значений строковых атрибутов;
• частое повторение определенных последовательностей символов;
• частое появление символов или последовательностей символов в определенных местах (позициях).

Для табличных данных характерны как вертикальные корреляционные связи (по столбцу), так и горизонтальные (по строке). Часто вертикальные зависимости сильнее горизонтальных. Лучшее сжатие будет обеспечиваться теми методами, которые эффективно эксплуатируют все типы избыточности.

Наиболее распространенными типами данных, используемыми в БД, являются строковые и числовые [14, 24, 32]. Такие типы, как дата и время, могут быть представлены как числовые. Часто методы сжатия данных числовых и строковых (текстовых) типов имеют специфику, поэтому они рассмотрены отдельно.

Кодирование числовых данных

Упаковка битов

Метод упаковки битов (bit packing) заключается в кодировании значения атрибута битовыми последовательностями фиксированной длины. Для каждого сжимаемого столбца требуется хранить соответствующую таблицу перекодировки. Разрядность кодовых последовательностей определяется количеством различных чисел, значения которых реально принимаются атрибутом, или же мощностью области определения атрибута. Очевидно, что требуемая длина кода равна , где  — это мощность множества реальных или допустимых значений атрибута. Данный метод рассматривается в одной из самых ранних статей по сжатию баз данных [3]. Метод упоминается наряду с другими приемами в [41] под названием “bit compression”.

Упаковка битов — это простой способ сжатия на уровне значения атрибутов, реализация которого необременительна. Также важно, что при соответствующей реализации сохраняется упорядоченность. Но проблемой при использовании данного метода является обработка появления новых значений атрибута. В этом случае может потребоваться перекодировать все значения столбца, если становится больше исходного . В работах [24, 25] предложена модификация метода для сжатия целых чисел, позволяющая в ряде случаев избежать перекодирования и естественным образом обеспечивающая сохранение упорядоченности. Алгоритм сжатия, названный автором “frame of reference compression” — “сжатие кадра ссылок”, состоит из двух частей:

• уровень страницы — сжатие строк и их сохранение в отдельных страницах;
• файловый уровень — перераспределение данных между страницами с учетом способа сжатия уровня страницы для улучшения общей степени компрессии.

Данные, физически перераспределяемые при обработке на файловом уровне, кодируются при обработке на уровне страницы.

Суть метода: для каждого столбца находится минимальное и максимально значение. Значения, попавшие внутрь этого диапазона, последовательно кодируются. Длина кодового слова постоянна и определяется размером диапазона. Пример: пусть имеется последовательность строк из двух полей

 = {(100, 21), (98, 24), (103, 29)}.

Для первого поля диапазон [98, 103], для второго — [21, 29]. Мощность первого множества значений равна 6, второго — 9. Поэтому будет представлена как:

 = {(010₂, 0000₂), (000₂, 0011₂), (101₂, 1000₂)}.

Очевидно, что если сжатие применяется к полям фиксированной длины, то их новая длина также фиксирована. Для каждого столбца необходимо хранить только границы диапазона и, возможно, длину. Перекодирование требуется лишь в случае выхода значения за границы диапазона.

Степень сжатия сильнее всего зависит от распределения значений каждого атрибута для записей, хранящихся в одной странице. Можно кардинально улучшить сжатие за счет перераспределения записей по страницам при обработке на файловом уровне.

В [24] предлагается применять алгоритм сжатия кадра ссылок и для экономного кодирования индексных структур древовидного вида. В частности, рассмотрено сжатие структур типа R-деревьев⁷, в том числе с потерями информации внутри индекса. Последнее позволяет достигать компромисса между используемым объемом внешней памяти для хранения индекса и скоростью поиска. Структура R-дерева такова, что сжатие с потерями не приводит к неоднозначности результатов поиска.

В [25] указывается, что предложенный алгоритм позволил сжать таблицы с данными о фондовых операциях в 3-5 раз. Скорость выполнения запросов при выборке данных в десятки раз превосходила вариант, при котором для сжатия использовался алгоритм типового компрессора Gzip. Экономное кодирование R-деревьев в БД одной геоинформационной системы уменьшило размер их представления до 55% от исходного.

Кодирование целых чисел через разницу между их значением и величиной нижней границы диапазона имеющихся значений атрибута также использовано в [14].

Метод упаковки битов не может обеспечить значительной степени сжатия относительно других методов, что, тем не менее, во многих приложениях может компенсировать высокой скоростью обработки данных и сохранением упорядоченности.

Кодирование длин серий и методы устранение констант

В общем случае, основной выигрыш при кодировании числовых данных может быть получен за счет сжатия ведущих нулей и экономного кодирования часто повторяющихся значений, которыми обычно являются ноль и отсутствующее значение [49, 36, 57]. Такие часто повторяющиеся значения называются в этом подпункте константами. Сжатие ведущих нулей часто выполняется с помощью упаковки битов, рассмотренной в предыдущем подпункте.

Последовательности констант при кодировании длин серий заменяются на тройки <флаг, константа, длина серии> [3, 36]. Существуют другие модификации метода, но общим недостатком является медленное декодирование, требующее операций, где  — число элементов исходной строки [36].

Устранение определенной константы может быть реализовано с помощью битовой карты. При этом физически в БД сохраняются только неконстантные значения. Местоположение констант определяется битовой картой, каждый разряд которой равен, например, 1, если в соответствующей позиции находится обычное значение, и 0, если константа. Например, если исходная строка , то сжатая строка и битовая карта . Как и для кодирования длин серий, время декодирования равно [36].

В работах [21, 22] была предложена модификация метода битовой карты, обеспечивающая в среднем более быстрый поиск в сжатых данных. В этом методе, названном “заголовочное сжатие”, битовая карта преобразована в заголовочный вектор , в нечетных позициях которого записывается число несжатых значений с накоплением, а в четных — число пропущенных констант с накоплением. Например, для исходной строки вектор . Декодирование информации может быть выполнено посредством бинарного поиска по , поэтому время декодирования пропорционально [36].

В [36] описана более сложная модификация метода битовой карты, позволяющая сократить число обращений к внешней памяти при декодировании. Метод назван “BAP”, поскольку при сжатии используется три объекта: битовый вектор (bit vector, BV), адресный вектор (address vector, AV) и так называемый физический вектор (physical vector, PV). В позиции битового вектора записывается 0, если текущий символ равен константе, и 1, если наоборот. В физическом векторе перечисляются все неконстантные значения. Битовый вектор разбивается на подвектора, каждый из которых независимо сжимается с помощью кода Голомба⁸ и сохраняется в отдельном блоке или последовательности блоков устройства внешней памяти. В ячейке адресного вектора хранится относительная позиция в физическом векторе последнего неконстантного элемента для подвектора с номером . Первый элемент адресного вектора равен нулю. Если в предыдущем подвекторе одни константы, то в адресный вектор записывается значение его предыдущего элемента. Адресный вектор также может быть сжат с помощью дифференциального кодирования. При кодировании и декодировании на основании адресного вектора определяется, какой подвектор надо распаковать, и декодируется только он. Если адресный вектор достаточно мал, чтобы поместиться в оперативную память, то при декодировании требуется только одно обращение к внешней памяти.

Например, если размер подвектора равен 5, и константа есть “0”, то для строки

содержимое векторов будет таким:

,

,

.

В частности, , поскольку последний неконстантный элемент 4-го подвектора содержится в . Это число 12.

Варьируя параметры, можно задавать соотношения между числом обращений, размером адресного вектора, размером блока, максимальной степенью сжатия и максимальным размером БД.

В [36] приведены результаты практического сравнения методов по степени сжатия. BAP выиграл у битовой карты в рассмотренных случаях. BAP работал стабильнее кодирования длин серий и сжатия заголовков, выигрывая у этих методов при отсутствии кластеризации неконстантных значений или констант в непрерывные серии по несколько сотен символов и более.

Следует подчеркнуть, что экономное кодирование констант актуально только для сильно разреженных БД. Например, такое свойство характерно для БД, в которых накапливаются данные о физических экспериментах.

Статистическое кодирование

Статистическое кодирование именно числовых данных редко упоминается в публикациях. Методы арифметического сжатия, кодирования по Хаффману и другие способы статистического кодирования применялись к данным произвольного типа. В [3] рассмотрена простая схема сжатия чисел посредством использования кода переменной длины, строящегося на основании статистики встречаемости чисел. Множество чисел разбивается на группы в соответствии с частотой использования так, что в группы малого размера попадают часто используемые значения. Элементы в пределах группы кодируются словами одинаковой длины , где  — размер группы. Кодовые слова разных групп различаются за счет использования флагов или префиксов. Такая схема обеспечивает в общем случае худшее сжатие, чем алгоритм Хаффмана, но может требовать меньше времени для кодирования.

Статистическое кодирование в силу достаточного затратного декодирования может иметь преимущество только при большой статистической избыточности числового массива и необходимости обеспечения высокой степени сжатия. Последнее требует применения сравнительно сложного моделирования, иначе более выгодным будет словарный подход к сжатию.

Дифференциальное кодирование

При обычном дифференциальном кодировании на уровне строки значение -ой строки -го столбца заменяется на разность . Если в пределах колонки имеется значимая тенденция в изменении данных, то результирующие разности могут быть экономно представлены с помощью простых методов.

В [37] описано применение дифференциального кодирования для сжатия БД с информацией о веществах-кандидатах для создания лекарств. БД используется для обеспечения процесса поиска лекарства для заданной болезни. Каждое вещество может характеризоваться тысячами признаков. Необходимость хранить описания нескольких миллионов веществ приводит к получению БД объемом в десятки гигабайт, что обуславливает актуальность экономного кодирования для уменьшения размера БД и повышения скорости выполнения запросов. Основная таблица БД состоит из трех числовых столбцов: номер вещества-кандидата, номер признака, собственно значение признака (может принимать отсутствующее значение). Значение признака вещества вещественное. При работе с БД используется как, главным образом, случайный доступ, так и последовательный. Новые записи вносятся редко и сразу большими массивами.

Отмечается, что использование схемы дифференциального кодирования, предложенной в [41], непрактично для рассматриваемой БД, поскольку в указанном алгоритме предполагается, что области определения атрибутов небольшие по мощности и заданы заранее. Предложенная схема сжатия, названная “сжатие окна” (window-based compression), включает в себя следующие шаги при кодировании.

1. Сортировка данных по номеру вещества и номеру признака.
2. Группировка соседних записей в так называемые окна. За счет сортировки значения столбцов “номер вещества” и “номер признака” всегда располагаются в возрастающем порядке внутри окна, и разница между ними мала.
3. Значения столбцов “номер вещества” и “номер признака” заменяются на их разность с соответствующими значениями первой строки окна, которая остается в исходном виде.
4. Полученные строки кодируются. Каждый символ представляется 4-битовым кодовым словом. При этом наиболее часто встречаемая пара символов кодируется одним словом.

Размер окна было решено выбрать переменным, так что в пределах одного окна все записи имеют одинаковое значение столбца с номером вещества.

Оценка эффективности сжатия проводилась с помощью специально разработанной СУБД, поддерживающей обновление записей и индексирование данных. Было произведено сравнение эффективности применения кода постоянной длины и кода Хаффмана для шага 4. Указывается, что использование кода Хаффмана не привело к повышению общей производительности работы с БД. Степень сжатия типовой БД веществ-кандидатов при использовании предложенной схемы составила 3.55 раза, при этом, для сравнения, степень сжатия для компрессора Gzip равнялась 5.3 раза. Приведены следующие характеристики изменения скорости выполнения запросов, считающих данные, из-за использования сжатия:

• при отсутствии индексов скорость для случайного доступа в 4 раза выше относительно скорости для несжатой БД, скорость для последовательного — в 2 раза;
• при наличии индексов скорость случайного доступа на 300-20% выше скорости при несжатой БД (чем больше число читаемых записей, тем разница меньше), скорость последовательного — ниже на 10-15%.

Для сравнения указывается, что запросы, требующие случайного доступа, выполняются посредством разработанной тестовой СУБД в 2 раза быстрее, чем Oracle 8i. Известно, что в данной версии Oracle поддерживается только сжатие индексов (см. параграф “Oracle” раздела “2. Использование сжатия данных в современных СУБД”).

Делается вывод, что сжатие использовать не нужно, если чтение из индексированной базы главным образом последовательное. Если используется случайный доступ, то сжатие может троекратно увеличить скорость.

Дифференциальное кодирование как средство учета вертикальных зависимостей является одним из основных способов сжатия данных в СУБД и часто используется в качестве одного из шагов алгоритма сжатия. Главный недостаток метода состоит в сложности обеспечения случайного доступа, поскольку для декодирования необходимо знать базовое значение.

Кодирование текстовых данных и данных произвольного типа

Метод Хаффмана

Метод Хаффмана как один из основных и наиболее популярных способов экономного кодирования неоднократно рассматривался применительно к задаче сжатия в СУБД.

В [50] описывается использование кодирования по Хаффману для решения практической задачи сжатия БД с заявками на приобретение продукции. Требовалось обеспечить степень сжатия в 2 и более раз, программа реализации кодирования и декодирования должна была иметь малый размер, устанавливалось жесткое ограничение на время декодирования записи. БД содержала колонки как строкового, так и числового типов, причем значения столбцов редко повторялись. В качестве кандидатов рассматривались варианты кодирования длин серий, словарного кодирования, схемы статистического сжатия. В итоге всем ограничениям удовлетворил только неадаптивный алгоритм Хаффмана с расширением алфавита символов. Для улучшения сжатия к 64 символам алфавита были добавлены 12 часто встречающихся последовательностей символов. В результате была достигнута степень сжатия 2.58 раза. При этом ключевые столбцы и те столбцы, по значениям которых часто производились выборки, были оставлены незакодированными. Словарный алгоритм, продемонстрировавший аналогичную степень сжатия, был отсеян по критериям скорости декодирования и размеру программы.

В [3] метод Хаффмана рассматривается наряду с другими более простыми приемами сжатия табличных данных.

В [20] для улучшения сжатия табличных данных по методу Хаффмана было предложено использовать отдельные распределения частот для различных типов данных, получаемые на основании выборок из таблиц. Для обеспечения большей скорости разжатия использована модификация кода Хаффмана с длиной слов, кратной байту (максимум 2 байта). Сжатие производилось на уровне строки, т.е. не обеспечивался доступ к закодированным значениям отдельных атрибутов. Выбор распределения частот и, соответственно, кода Хаффмана для сжатия очередного элемента производился на основании предыдущего обработанного символа. Если предыдущий символ причислялся к типу данных , то для кодирования текущего символа использовалось распределение частот для . Указано, что степень сжатия для предложенного алгоритма составила 2 раза, количество операций ввода-вывода уменьшилось на 32.7%, при этом число используемых тактов процессоров выросло только на 17%. Данный алгоритм использовался в СУБД IMS фирмы IBM [20, 32].

В чистом виде метод Хаффмана не может конкурировать со словарными схемами по степени сжатия, что предопределяет его нишу вспомогательной техники. Достоинство подхода в простоте и скорости декодирования. Метод допускает простую аппаратную реализацию.

Арифметическое сжатие

В работе [47] на основе сравнительного анализа эффективности различных схем сжатия было установлено, что полуадаптивное арифметическое кодирование обладает преимуществом в изученных ситуациях с точки зрения обеспечиваемого сжатия. Автором работы предлагается использовать в СУБД алгоритм арифметического кодирования на уровне значения атрибута с отдельной моделью для каждого столбца.

Сравнивались методы: кодирование длин серий (КДС), адаптивный вариант LZW, адаптивное и полуадаптивное арифметическое кодирование (ААК и ПАК), адаптивное и полуадаптивное кодирование по Хаффману (АКХ и ПКХ). Сопоставление производилось на трех наборах данных, описанных в Таблица 1, и при различных уровнях гранулярности. Размер страницы был положен равным 4 кБайт. Полуадаптивные алгоритмы ПАК и ПКХ опирались на статистику, собранную со всей таблицы. Для ПАК также рассмотрен вариант, при котором статистика собиралась отдельно для каждого столбца. В этом случае использовалось несколько распределений. Результаты сравнения по степени сжатия представлены в Таблица 2. Приводимые сведения интересны в первую очередь тем, что позволяют оценить влияние гранулярности на степень сжатия данных разных типов.

Таблица 1

Название	Описание таблицы
PUB	Библиография научных публикаций. 11 строковых атрибутов (имена авторов, наименование, издательство и т.п.) и 80690 записей. Длина записи 1828 байтов, при этом средняя длина значений большинства строковых атрибутов значительно меньше максимальной ширины соответствующих столбцов.
BANK	Банковская информация о счетах клиентов. 24 атрибута, из которых 19 строковых и 5 числовых, и 55862 записи. Длина записи 236 байтов.
SYN	Искусственно сгенерированная таблица. 12 атрибутов, из которых 11 числовых и 1 строковый, и 9964 записи. Длина записи 76 байтов. При генерировании числовых значений использовались распределения, полученные из статистики по некоторым таблицам с реальными данными.

 

Таблица 2

Таблица	Метод	Степень сжатия при разных уровнях гранулярности
		Файл	Страница	Строка	Значение атрибута	Значение атрибута, разные распределения
PUB	КДС	5.09	5.00	4.78	4.44
	LZW	11.86	5.85	4.80	3.36
	ААК	4.87	4.18	3.62	2.50
	ПАК	4.72	4.69	4.55	4.27	4.89
	АКХ	4.10	3.84	3.55	2.99
	ПКХ	3.99	3.98	3.91	3.60
BANK	КДС	1.32	1.32	1.28	1.12
	LZW	5.26	2.86	1.58	0.84
	ААК	2.06	1.94	1.42	0.94
	ПАК	1.87	1.86	1.81	1.36	1.79
	АКХ	1.99	1.90	1.55	0.97
	ПКХ	1.77	1.77	1.70	1.40
SYN	КДС	1.27	1.27	1.23	1.04
	LZW	1.86	1.68	1.26	0.75
	ААК	1.79	1.74	1.26	0.83
	ПАК	1.80	1.80	1.67	1.24	1.27
	АКХ	1.79	1.63	1.16	0.97
	ПКХ	1.78	1.78	1.66	1.26

Из Таблица 2 следует, что в случае текстовых полей сжатие достигается в первую очередь за счет экономного кодирования оконечных пробелов, принудительно увеличивающих длину значения до заданной ширины столбца. Если СУБД поддерживает строковые атрибуты переменной длиной, то эффект от КДС должен становиться в большинстве случаев крайне незначительным. LZW плохо работает на таблицах с колонками малой ширины. Адаптивные методы ААК и АКХ неэффективны на уровне страницы и приводят к увеличению объема данных при сжатии на уровне значений атрибутов. При малых уровнях гранулярности — строка и столбец, наилучшим образом подходящих для эффективного выполнения запросов, стабильно хорошие результаты показывают ПАК и ПКХ. Поскольку ПАК обеспечивает существенно лучшее сжатие текстовых данных, автор [47] выбирает этот метод в качестве базового для создания новой схемы сжатия. В этой схеме, названной в [48] “COLA” (Column-Based Attribute Level Non-Adaptive Arithmetic Coding — “неадаптивное арифметическое кодирование уровня атрибута по колонкам”), значение атрибута арифметически кодируется на основании распределения частот, полученного для данного атрибута. Характеристики степени сжатия для такой схемы представлены в последней колонке Таблица 2.

Тем не менее, в [47] не дается сравнительных оценок скорости кодирования и, главное, декодирования. Поскольку декодирование для арифметического сжатия сложнее, чем для алгоритма Хаффмана, то выбор в пользу арифметического кодирования представляется недостаточно обоснованным. Характеристики производительности являются первостепенными. Например, в [32] при выборе алгоритма сжатия для СУБД DB2 предпочтение было отдано методу семейства Зива-Лемпела, который при сходной степени сжатия обеспечивал бо́льшую скорость декодирования, чем использованная схема арифметического сжатия.

В [8] имеется краткое упоминание об эксперименте по применению арифметического кодирования для сжатия БД. Для учета неоднородности данных в пределах строки, обусловленной разным характером данных отдельных столбцов, авторы предложили использовать несколько алфавитов. Это позволяет ускорить процесс адаптации к локальным особенностям информации. Отмечено увеличение степени сжатия на 12% при тестировании на файлах СУБД Ingres.

Следует отметить, что использование арифметического кодирования в СУБД может быть перспективным, поскольку арифметическое кодирование сохраняет порядок сортировки элементов в соответствии с их накопленной вероятностью, если упорядоченность не жертвуется в пользу ускорения обработки [6, 61]. В [35] описана модификация алгоритма арифметического кодирования для решения задачи сжатия исполнимого кода с возможностью декодирования “на лету”. Разработанный алгоритм обеспечивает случайный доступ к сжатым данным с точностью до блока задаваемого размера. Предложенная схема позволила получить бо́льшую степень сжатия, чем алгоритм Хаффмана, при сходной скорости декодирования. При этом использовалась полуадаптивная модель, размер блока составлял 4..64 байта. Очевидно, что разработанный алгоритм соответствует требованиям, предъявляемым к методам экономного кодирования для их использования в СУБД.

Методы Зива-Лемпела

Вопрос использования методов Зива-Лемпела для сжатия данных в СУБД исследован, в частности, в работах [32, 47]. Авторы приходят к заключению, что методы Зива-Лемпела непрактичны для сжатия на уровне значения столбца. В [32] также указывается, что адаптивные методы проигрывают по степени сжатия неадаптивным (полуадаптивным).

В [32] для использования в СУБД предложен вариант метода Миллера-Уэгнама (Miller-Wegnam), или LZMW [1]. В методе Миллера-Уэгнама каждая фраза словаря представляет собой конкатенацию двух других фраз, а не фразы и символа алфавита данных, что отличает метод от LZW. Сжатие в предложенной схеме выполняется на уровне строки и является полуадаптивным. Словарь строится при загрузке данных и может иметь размер до 4096 фраз. Указывается, что использование сжатия позволило сократить размер типовых БД в 2 раза при аналогичном увеличении скорости выполнения запросов. Расход тактов процессора увеличился всего на 20%. Данная схема была реализована в СУБД DB2 фирмы IBM. Подробнее см. параграф “DB2” раздела “2. Использование сжатия данных в современных СУБД”.

Методы Зива-Лемпела часто использовались как эталонные при сравнении схем сжатия данных. Так, в [41] производится сравнение эффективности LZW с другими методами сжатия применительно к задаче экономного кодирования в СУБД. Аналогичную роль играет компрессор Gzip, реализующий метод LZH, в [24, 11, 37].

В [61] рассмотрена схема модификации метода LZW, позволяющая достичь свойства сохранения упорядоченности. Упорядоченность теряется при назначении разных кодовых слов строкам, которые являются префиксами друг друга. Поэтому для обеспечения сохранения порядка сортировки в словарь добавляются фразы, образуемые слиянием имеющихся фраз и “пустого” символа (“zilch”), не принадлежащего алфавиту данных. Эта модификация выполняется только для фраз, которые являются префиксами других фраз словаря. Указано, что предложенный прием применим к любым словарным схемам типа LZ78, задающим отображение исходной последовательности переменной длины в кодовое слово фиксированный длины, если все символы алфавита данных являются фразами словаря.

Основным недостатком методов Зива-Лемпела является сложность обеспечения произвольного доступа к информации.

Другие способы словарного сжатия

Сжатие табличных данных посредством словарного кодирования на уровне значений атрибутов часто изучалось в исследованиях [3, 14, 17, 57]. Существует ряд практических реализаций таких схем сжатия в СУБД [40, 45]. В большинстве случаев словарь для сжатия отдельного столбца образуется из значений данного атрибута. Обычно фразами словаря делаются все имеющиеся значения. Кодирование при этом сводится к замене значения на номер соответствующей фразы словаря (указатель).

В диссертационной работе [14] предложен подход к сжатию строковых атрибутов под названием “иерархическое словарное кодирование”, в котором используется набор из конкурирующих алгоритмов сжатия, работающих на разном уровне гранулярности данных. Используются полуадаптивные алгоритмы словарного кодирования на уровне целого значения атрибута, которое часто является последовательностью слов, слова, префикса/суффикса слова и символа. Уровень детальности выбирается исходя из минимизации суммы размеров закодированной колонки и словаря. Таким образом, обеспечивается возможность эффективного учета различных типов избыточности. Для оценки жизнеспособности подхода было произведено его сравнение с другими словарными методами на данных теста TPC-H. В сопоставлении были задействованы реализации полуадаптивного алгоритма LZW, кодирования по словарю значений атрибута и кодирования по словарю из слов, встречающихся в значениях атрибута. Предложенный подход имел наибольшую эффективность среди рассмотренных методов, обеспечив двукратное сжатие при увеличении скорости последовательного доступа к данным на 30%.

Дифференциальное кодирование, векторное квантование

Дифференциальное кодирование для преобразования данных произвольного типа упоминается в обзорной статье [49]. Идея использования дифференциального кодирования получила развитие в рамках подхода по применению векторного квантования для преобразования и сжатия табличных данных [41, 42, 43].

Векторное квантование можно рассматривать как расширение дифференциального кодирования для многомерного случая. Суть векторного квантования заключается в разбиении множества объекта на группы по некоторому критерию сходства. Среди объектов каждой группы выбирается один, выражающий наиболее характерные свойства объектов группы (образцовый объект). В результате векторного квантования все объекты группы приравниваются к образцовому. Если требуется выполнить преобразование без потерь, то сохраняется разница между текущим и образцовым объектами. Это и определяет родство с дифференциальным кодированием.

В [42, 43] предложен способ использования векторного квантования для безущербного сжатия в СУБД. Способ был разработан для экономного кодирования баз статистических данных. В [41] подход к сжатию был пересмотрен, и результирующий алгоритм стал фактически эквивалентеным дифференциальному кодированию.

Отдельная строка таблицы рассматривается как точка в -мерном пространстве, образованном декартовым произведением всех атрибутов. Например, если имеются два атрибута, и их множества значений и , то пространство состоит из 6 точек: . Очевидно, что мощность .

Процедура сжатия состоит из нескольких шагов.

1. Все строки упорядочиваются в соответствии с правилами упорядочивания отдельных атрибутов. Например, если атрибут строковый, то его значения располагаются в словарном (лексикографическом) порядке. Каждой строке ставится в соответствие ее порядковый номер в полученной последовательности кортежей. Иначе говоря, с помощью некоторой функции 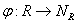, где 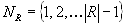, производится отображение 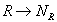, каждой строке 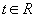ставится в соответствие 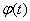. Для обеспечения лучшей результирующей степени сжатия рекомендуется составлять 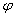так, чтобы сначала сортировать строки по атрибутам с большим количеством значений.
2. Массив строк разбивается на блоки. Размер блока принимается равным величине страницы таблицы. Внутри блока все строки упорядочены.
3. Блоки кодируются. Первая строка 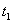оставляется в исходном виде, т.е. выполняет роль образца. Другие строки 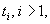кодируются через разность 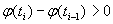. Разность записывается в позиционной системе счисления с весами 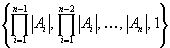. Для улучшения сжатия последовательность ведущих нулей кодируется через указание ее длины. Например, если 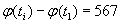, , 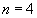мощности множеств 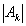равны 4, 3, 64, 100 соответственно, то разность представляется как 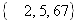, поскольку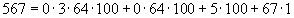

. Два ведущих нуля обозначены первой цифрой.

Если атрибуты не являются целыми числами, то для преобразований и может потребоваться поддерживать таблицу соответствия между значением атрибута и его номером в отсортированной последовательности значений. В [41] предлагается для каждого такого атрибута создавать словарь из всех используемых значений.

Таким образом, сжатие достигается за счет:

1. упаковки битов (или словарного перекодирования) при переходе от значений атрибутов к порядковым номерам;
2. кодирования длины серии ведущих нулей, часто образующейся в результате взятия разности.

В [41] приведены оценки эффективности предложенного подхода для БД результатов обследования домохозяйств Бюро переписи населения США. Указывается степень сжатия 4 раза при увеличении скорости выполнения запросов на 41.3%. Использование для сжатия данных алгоритма LZW привело к получению аналогичной степени сжатия, но повышение скорости работы составило только 35.2%.

В более ранней работе [42] в качестве образцовой строки выбиралась строка , находящаяся посередине блока, а прочие строки кодировались через разность 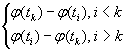. Это точнее соответствует сути векторного квантования. Для повышения степени сжатия выполнялся второй этап взятия разности: текущая строка характеризовалась результатом вычитания ее разности из разности предыдущей строки. Из сравнения результатов экспериментов, приводимых в [42] и [41], следует, что при использовании чистого векторного квантования степень сжатия меньше примерно на 10%, а скорость декодирования ниже на несколько десятков процентов. Таким образом, применение дифференциального кодирования оказалось более предпочтительным в рамках проведенных исследований.

Как уже отмечалось, векторное квантование и дифференциальное кодирование актуальны как средства простого учета вертикальных взаимосвязей в данных, но при их применении усложняется организация эффективного произвольного доступа к информации.

Сортировка, группировка и преобразование столбцов

Сортировка значений как предварительная операция позволяет применять к полученным данным простые методы сжатия. Но при сжатии без потерь необходимо иметь возможность восстановить исходный порядок при декодировании.

Сортировка в пределах колонки или набора колонок может быть легко обращена, если эти колонки функционально зависят от известной опорной группы колонок . Тогда значения сортируются по значениям . В этом случае лексикографически отсортированные значения дадут индекс, позволяющий обратить сортировку. В примере ниже {ID}, {Город}.

№ строки	ID	Город	Отсортированная опорная колонка "ID"	Колонка "Город", отсортированная по ID	Индекс для восстановления
1	1	Москва	1	Москва	1
2	2	Санкт-Петербург	1	Москва	3
3	1	Москва	1	Москва	4
4	1	Москва	1	Москва	6
5	2	Санкт-Петербург	2	Санкт-Петербург	2
6	1	Москва	2	Санкт-Петербург	5

Для однозначного восстановления сортировка должна быть устойчивой, с сохранением порядка одинаковых элементов. Стоит отметить, что такой прием используется и при обратном преобразовании Барроуза-Уилера [1].

В [57] предложен эффективный субоптимальный алгоритм нахождения дерева зависимости групп колонок от некоторой пары других колонок. Оценка полезности сортировки основана на подсчете длин серий, возникающих при сортировке. Авторы указывают, что учет функциональной зависимости только максимум от колонок хорошо работает на практике. В то же время задача определения оптимального разбиения при является НП-трудной, т.е. число шагов алгоритма полиноминально растет с увеличением числа столбцов. Показано, что предложенная схема позволяет кардинально улучшить сжатие табличных файлов не только относительно универсальных компрессоров, но и специализированного табличного компрессора, описанного в [11].

Известно, что перестановка столбцов может существенно улучшить сжатие при построчной обработке. Для нахождения оптимальных группировок в [11] предложено кодировать небольшой обучающий фрагмент данных и использовать статистику для решения задачи с помощью динамического планирования (программирования). Для ускорения процедуры оптимизации столбцов разбиваются на попарно непересекающихся групп. Это позволяет получить субоптимальный результат при временной сложности вместо ). Для исследованных данных потери в результирующей степени сжатия крайне малы в том случае, когда и отличаются только в разы, т.е. .

В [11] также рассмотрено дифференциальное кодирование на уровне столбцов при сжатии данных произвольного типа. Для данных, рассматриваемых в указанной публикации, характерно, что значения некоторого исходного столбца таблицы сжимаются слабее, чем результат преобразования , где – опорный столбец. Взятие используется как предварительный этап перед кодированием с помощью LZH.

Другие методы сжатия данных

Способ экономного кодирования данных на основе грамматической модели был предложен в [12]. Созданный алгоритм, названный авторами RAY, основан на достаточно известном алгоритме универсального сжатия данных SEQUITUR⁹. В SEQUITUR реализуется автоматическое адаптивное построение контекстно-свободной грамматики для обрабатываемых данных. По сути SEQUITUR является словарной схемой сжатия, в которой каждая фраза словаря соответствует некоторому правилу грамматики.

В отличие от SEQUITUR, RAY является многопроходным полуадаптивным алгоритмом. В результате каждого этапа просмотра данных выполняется модификация грамматической модели: добавляются новые правила и изменяются при необходимости существующие. Утверждается, что многопроходное построение модели позволяет сократить расходы оперативной памяти и обеспечивает возможность выбора между скоростью и степенью сжатия за счет варьирования числа этапов. Как и в SEQUITUR, минимальная длина правой части грамматического правила (продукции) равна двум символам. Но, если в SEQUITUR для создания правила требуется двукратное появление пары, в RAY используется переменный порог частоты встречаемости во всем массиве данных. Величина порога зависит от номера этапа. После каждого этапа правила грамматики кодируются по алгоритму Хаффмана. Собственно обрабатываемая последовательность, которая является первым правилом грамматики и включает в себя ссылки на другие правила (т.е. номера правил), кодируется сходным образом.

В [12] приведены результаты сравнения RAY с другими алгоритмами на данных трех типов. Отмеченная степень сжатия примерно на 20% выше степени сжатия для компрессора Gzip, но при этом скорость декодирования в 2-4 раза ниже. Из статьи не ясно, каким образом обеспечивалось независимое декодирование отдельных записей таблиц. Возможно, что приведенные результаты соответствуют варианту сжатия файлов целиком, без поддержки случайного доступа к записям. Таким образом, существующая реализация дает лишь незначительный выигрыш в степени сжатия над неспециализированным компрессором Gzip, но существенно уступает ему же в скорости декодирования. В таком виде алгоритм не может быть реальным кандидатом для организации сжатия данных в СУБД.

Сжатие табличных данных с потерями

Сжатие табличных данных с потерями информации допустимо в некоторых приложениях, например, при разведочном анализе больших массивов данных.

Идея рассмотренных в литературе методов сжатия с потерями, предлагаемых к применению в СУБД, заключается в построении модели, как можно точнее описывающей все строки. Модель задает преобразование , позволяющее по некоторым аргументам получить строку , принимаемую за исходную . Сжатые данные должны содержать описание , и, возможно, некоторые исходные строки , отличие которых от модельных больше заданного порогового значения некоторого критерия.

Для сжатия с потерями предлагались методы кластерного анализа [46]. Под кластером¹⁰ понимался набор строк, для которых значения некоторых атрибутов сходны. Порог сходства для объединения записей в кластеры и число сходных атрибутов задается пользователем. Поэтому правило формирование кластеров определяется как , где  — число сходных атрибутов,  — порог сходства. Для числовых атрибутов определяет максимальную ширину диапазона значений, для категориальных — предельное число различных значений. Сжатие достигается за счет того, что для каждой строки кластера сохраняются только значений несходных атрибутов. Значения сходных атрибутов усредняются по всему кластеру. Вычисленные репрезентативные значения разделяются всеми строками кластера. Таким образом, значения атрибутов сохраняются сразу для множества записей. С целью ускорения работы авторы алгоритма предложили строить кластеры, опираясь на центры сетки, “натянутой” со случайным шагом на множество всех возможных кластеров для конкретной таблицы. Это позволяет получить однопроходный алгоритм. Проблемой метода является задача выбора и невозможность учета строки в нескольких кластерах, что ухудшает сжатие.

В [46] также рассмотрен усовершенствованный кластерный метод “ItCompress”, обеспечивающий лучшее сжатие при сходном уровне ошибки. Для каждого кластера выбирается “образцовая” запись как репрезентативный представитель. Если значение атрибута строки кластера отличается от значения атрибута образцовой записи на допустимую величину, то значение не сохраняется. Если ошибка аппроксимации велика, то такое значение-выброс запоминается. В результате сжатия для каждой строки кластера указываются: идентификатор образцовой строки кластера, битовый вектор описания значений, список значений-выбросов. Разряд битового вектора равен 1, если значение соответствующего атрибута приравнивается образцовому, и 0, если соответствующий атрибут имеет значение-выброс.

В [7] предложена схема сжатия с потерями на основе метода деревьев классификации и регрессии (Classification and Regression Tree, CaRT), названная SPARTAN. Подобно классической регрессии, метод позволяет приближенно предсказать значения некоторых атрибутов по значениям других атрибутов, играющих роль предикторов. В соответствии с предложенной схемой, если ошибка предсказания меньше задаваемого пользователем порога, то все колонки предсказываемых атрибутов целиком не сохраняются в БД. Записываются только описания моделей и колонки атрибутов-предикторов. Для ускорения процесса сжатия модели строятся для случайных выборок, а не для таблицы целиком. Недостатком подхода является используемое предположение об одинаковой силе и типе зависимостей между атрибутами в пределах всей таблицы. Если бы схема позволяла работать на уровне отдельных групп строк, это, очевидно, в общем случае увеличило бы степень сжатия при одновременном уменьшении ошибки аппроксимации.

Из [7, 46] следует, что схемы ItCompress и SPARTAN демонстрируют примерно одинаковую степень сжатия при сходной величине ошибки. На данных, использованных для сравнения, схемы обеспечивают степень сжатия порядка 5 при ошибке аппроксимации 1%. Степень сжатия аналогичных данных без потерь с помощью компрессора Gzip меньше примерно на 20%. Повышение порога допустимой ошибки до 10% увеличивает степень сжатия до 10-12 раз. При равных условиях ItCompress обеспечивает в 3-4 раза бо́льшую скорость кодирования и декодирования.

В [34] обсужден вопрос эффективного сжатия с потерями баз данных, содержащих временные ряды. Считается, что исходные временные ряды сохраняются по строкам матрицы (таблицы) . Столбцы соответствуют моментам (интервалам) времени. Предложен метод сжатия с потерями на основе сингулярного разложения (UV-разложения, разложения на собственные числа и собственные вектора) матрицы:

,

где  — матрица размера ( рядов, моментов времени), ;

 — матрица ортонормированных собственных векторов матрицы , размер ;

 — матрица ортонормированных собственных векторов матрицы , размер ;

 — диагональная матрица собственных значений матрицы , размер .

Разложение можно записать в такой форме:

.

Исходя из свойства разложения, чем меньше номер слагаемого, тем бо́льшую часть дисперсии исходных векторов, образующих матрицу , это слагаемое определяет. Соответственно, тем больше это слагаемое значимо. Сжатие в предлагаемой схеме достигается за счет сохранения только первых слагаемых ( главных компонент). выбирается исходя из заданного порога ошибки аппроксимации. Из приводимых в [34] результатов экспериментов следует, что степень сжатия протестированных наборов данных для предложенного метода составила 40 раз при средней ошибке в 5% и 10 раз при средней ошибке в 2%. Для сравнения, компрессор Gzip обеспечил безущербное сжатие рассмотренных таблиц в 4 раза.

Содержание | Часть 1 | Часть 2 | Часть 3 | Часть 4

 

Подстрочные примечания

⁷ R-дерево (R-tree) — сбалансированная древовидная структура данных, разработанная специально для индексирования многомерных пространственных объектов.
⁸ Код Голомба позволяет оптимальным образом закодировать неотрицательные целые числа, имеющие геометрическое распределение. В данном случае числа — это длины серий нулей. Код предложен в [S.W. Golomb. Run-length encodings. IEEE Transactions on Information Theory, vol. 12, pp. 399-401, July 1966]. Доказательство оптимальности имеется в [R. Gallager and D.V. Voorhis. Optimal source codes for geometrically distributed integer alphabets. IEEE Transactions on Information Theory, vol. 21, pp. 228-230, Mar. 1975].
⁹ См., например: Nevill-Manning C. Inferring Sequential Structure. PhD Thesis, University of Waikato, May 1996.
¹⁰Авторы алгоритма используют термин “fascicle” — «гроздь, пучок».